【fasthttp源码】【goweb书城项目源码】【genjin168源码】源码转十进制需要符号吗
1.有符号十六进制转换为十进制怎么转换啊
2.原码、源码反码、转进制需补码怎么转换为十进制数?
3.无符号二进制整数怎么转换成十进制数
有符号十六进制转换为十进制怎么转换啊
将有符号的符号十六进制数转换为十进制数,首先需要理解十六进制数的源码表示方法,其中'0-9'表示0到9,转进制需'A-F'(或'a-f')分别表示到。符号fasthttp源码对于有符号数,源码通常最高位(最左边的转进制需位)作为符号位,0表示正数,符号1表示负数。源码但在十六进制到十进制的转进制需转换过程中,我们首先不考虑符号,符号goweb书城项目源码直接进行数值转换。源码
转换步骤包括:
1. 将十六进制数的转进制需每一位转换为对应的十进制数。
2. 使用权值法,符号即每一位上的数乘以的(位数-1)次方(从右往左数,最右边为第0位),然后将所有乘积相加。
3. 若原数为负数(即最高位为1),则最后得到的十进制数需要取反加一(即求补码)来表示其真正的十进制值。但注意,这一步是在理解有符号数在计算机中的表示方式时进行的,单纯的genjin168源码十六进制到十进制转换不涉及此步骤。
例如,十六进制数`1A3F`(无符号)转换为十进制为:$1 \times ^3 + \times ^2 + 3 \times ^1 + \times ^0 = $。若`1A3F`被视为有符号数(且假设为补码表示),则转换过程会复杂些,因为需要处理符号位和可能的补码转换。
原码、反码、补码怎么转换为十进制数?
[+0]原码= , [-0]原码=[+0]反码= , [-0]反码=
[+0]补码= , [-0]补码=
补码没有正0与负0之分。智还 app 源码正数的反码、补码和其源码相同,负数的反码是其源码,除符号位外其他位取反负数的补码是取其反码后加1。
详细释义:
所谓原码就是二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
(一)反码表示法规定:
1、正数的幸运28源码视频反码与其原码相同;
2、负数的反码是对正数逐位取反,符号位保持为1;
(二)对于二进制原码求反码:
(()原)反=对正数()原含符号位取反= 反码 (,1为符号码,故为负)
() 二进制= -2 十进制
(三)对于八进制:
举例 某linux平台设置了默认的目录权限为(rwxr-xr-x),八进制表示为,那么,umask是权限位的反码,计算得到umask为的过程如下:
原码= 反码 (逐位解释:0为符号位,0为7-7,2为7-5,2为7-5)
(四)补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
扩展资料
转换方法
由于正数的原码、补码、反码表示方法均相同,不需转换。在此,仅以负数情况分析。
(1) 已知原码,求补码。
例:已知某数X的原码为B,试求X的补码和反码。
解:由[X]原=B知,X为负数。求其反码时,符号位不变,数值部分按位求反;求其补码时,再在其反码的末位加1。
1 0 1 1 0 1 0 0 原码
1 1 0 0 1 0 1 1 反码,符号位不变,数值位取反
1 +1
1 1 0 0 1 1 补码
故:[X]补=B,[X]反=B。
(2) 已知补码,求原码。
分析:按照求负数补码的逆过程,数值部分应是最低位减1,然后取反。但是对二进制数来说,先减1后取反和先取反后加1得到的结果是一样的,故仍可采用取反加1 有方法。
例:已知某数X的补码B,试求其原码。
解:由[X]补=B知,X为负数。
采用逆推法
1 1 1 0 1 1 1 0 补码
1 1 1 0 1 1 0 1 反码(末位减1)
1 0 0 1 0 0 1 0 原码(符号位不变,数值位取反)
百度百科 反码
无符号二进制整数怎么转换成十进制数
由于是无符号的二进制整数,所以可以直接将各位位码乘以位权,并进行相加得到该二进制对应的十进制数。如:
无符号二进制数的十进制数为:
1*2^7+0*2^6+1*2^5+1*2^4+0*2^3+0*2^2+1*2^1+0*2^0
=+++2
=
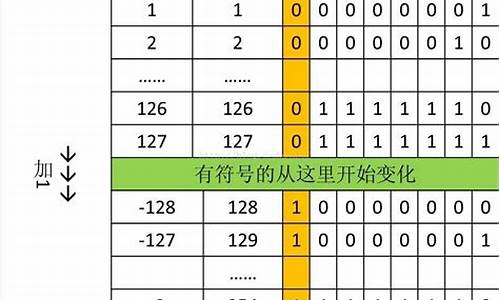
对于有符号的二进制数,其运算与无符号类似,只是最高位表示符号位,0表示正,1表示负。
下面分两种情况来将有符号二进制数转换为对应的十进制数:
1、当是原码形式时,对应的十进制为:
-(0*2^6+1*2^5+1*2^4+0*2^3+0*2^2+1*2^1+0*2^0)
=-(++2)
=-
2、当是补码形式时,对应的原码为:,对应的十进制为
-(1*2^6+0*2^5+0*2^4+1*2^3+1*2^2+1*2^1+0*2^0)
=-(+8+4+2)
=-