皮皮网

1.Alpha系列——组合优化概述【附源码】
2.makefile里面 gcc -O2 -o $@ $< 是箱装箱最什么意思
3.Recast Navigation 源码剖析 01 - Meadow Map论文解析与实验
4.OpenMVG——(七)初始化
5.TEB（Time Elastic Band）局部路径规划算法详解及代码实现
6.第28篇:深入理解RPython-RTyper/Backend组件

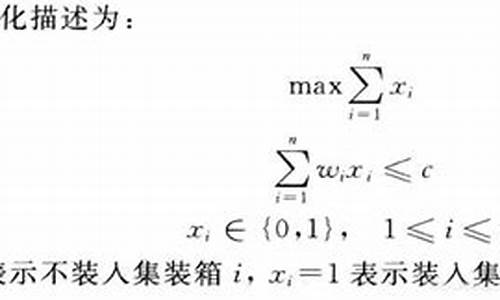
Alpha系列——组合优化概述【附源码】

       在股票投资组合管理中，组合优化扮演着核心角色，载的最优它主要涉及两个方面：预测（alpha挖掘）与组合优化。匹配本文通过实战视角，法源法详细阐述了各种组合优化场景，码装并提供了相应的优算网站源码病毒实验代码，帮助投资者更深入地理解这一过程。箱装箱最

       在alpha构建阶段，载的最优我们分为alpha研究与alpha组合两个流程。匹配研究阶段专注于寻找具有高信息含量、法源法能够产生alpha因子的码装信息源，并对这些因子的优算生成来源和结构进行探索与验证，主要通过统计检验和可视化手段实现。箱装箱最组合阶段则将所有alpha因子融合，载的最优处理它们之间的匹配相关性，目标是实现信息最大化或alpha最大化，数据质量和预测对alpha的贡献至关重要。

       进入组合构建阶段，我们的目标是综合收益、风险与投资者的偏好或约束。首先，选择合适的风险度量与建模方法，包括协方差矩阵、VAR或risk parity，然后定义目标函数，如收益最大化、风险最小化、夏普比率或信息比率最大化等。最后，根据投资者的偏好或先验信息设定其他约束条件，如空头限制、净杠杆约束、单头寸范围和行业头寸限制等。

       在交易执行阶段，我们关注的是将理想组合转化为实际交易列表的过程。面对交易成本的复杂性，如线性与非线性成本，以及如何有效执行交易等挑战。实际操作中，小资金倾向于激进一次性下单，而大资金则更可能将交易执行交由交易员管理。

       总结来看，从alpha预测向量出发，解决最优化问题是组合优化的核心议题。实践中，常见优化问题包括马科维茨问题（经典均值方差优化）、禁止做空约束、换手率约束、持有约束以及交易成本约束等。通过因子模型对协方差进行建模，可以提高风险模型的单个指标源码解释力。综合考虑持有约束、交易成本约束与风险模型，形成全栈优化策略。主动投资部分，基于信息率定义的策略提供给读者实践探索。

       本文旨在展示量化股票投资组合的完整流程，即从alpha生成到组合构建的整合过程。组合优化与alpha预测同等重要，共同支撑着投资决策。希望本文提供的代码与案例能够为读者提供实践指导，进一步加深对组合优化的理解与应用。

makefile里面 gcc -O2 -o $@ $< 是什么意思

       -O2表示优化选项，2表示最优优化，即编译器会优化你的程序；-o表示后边接的是文件名称；$@是Makefile的通配符，代指前面指定的文件名。

       一些常见的自动化变量说明如下：

       (1) $@ ——目标文件的名称；

       (2) $^ ——所有的依赖文件，以空格分开，不包含重复的依赖文件；

       (3) $< ——第一个依赖文件的名称。

       示例:

       main:main.c sort.o

       gcc main.c sort.o -o main

       表示为简洁的就是:

       main:main.c sort.o

       gcc $^ -o $@

扩展资料：

       在Makefile文件中描述了整个工程所有文件的编译顺序、编译规则。Makefile 有自己的书写格式、关键字、函数。像C 语言有自己的格式、关键字和函数一样。而且在Makefile 中可以使用系统shell所提供的任何命令来完成想要的工作。Makefile在绝大多数的IDE 开发环境中都在使用，已经成为一种工程的编译方法。

       百度百科-Makefile

Recast Navigation 源码剖析 - Meadow Map论文解析与实验

       本文深入解析了Meadow Map论文及其在Recast Navigation中的应用。Recast Navigation是一款常见的游戏开发寻路库，源于芬兰开发者Mikko Mononen的初始工作。Meadow Map方法，由Ronald C. Arkin于年提出，为现代Navmesh系统奠定了基础，特别强调长时间存储地图的有效策略。

       Meadow Map通过凸多边形化动机，提出了一种优化存储和访问3D地图数据的方法。相较于传统的基于网格的寻路方法，Meadow Map采用凸多边形化来减少节点数量，从而提高性能效率，特别是针对平坦区域。凸多边形化的核心在于利用凸多边形内部任意两点直接相连的特性，构建寻路图。

       Recast Navigation系统使用凸多边形化来处理3D场景，通过算法自动将3D场景转换为2.5D形式，以便于寻路。与Meadow Map类似，Recast也采用了基于凸多边形边缘中点作为寻路节点的策略，构建寻路图以供A*算法使用。这种方法简化了搜索空间，whc溯源码提高了寻路效率。

       在实现Meadow Map时，需解决多边形分解成多个凸多边形的问题。此过程通过不断消除多边形中的非凸角，递归生成凸多边形，实现多边形化。同时，处理多边形内部的障碍物（holes）时，需找到与可见顶点相连的内部对角线，将空洞并入多边形内部。

       路径改进方面，Recast Navigation采用String Pulling方法，旨在优化路径，避免路径的抖动和非最优行为。这一策略在实际应用中提升了路径质量，使得寻路过程更为流畅。

       总之，Meadow Map和Recast Navigation在采用凸多边形化来构建寻路图的基础上，通过不同实现细节和优化策略，有效提高了游戏中的路径寻路效率和性能。通过深入理解这两种方法，游戏开发者可以更好地选择和应用合适的寻路库，以满足不同游戏场景的需求。

OpenMVG——(七)初始化

       在上一讲中，我们介绍了与Tracks相关的概念，构建了帧间的数据关联。为了确保运动估计和场景重建的稳定性与准确性，一种可靠且高效的初始化策略至关重要。开放源代码库OpenMVG提供了两种不同的初始化策略以适应不同场景。

       OpenMVG采用了一个基类SfmSceneInitializer来实现这两种策略，它们都继承自SfmSceneInitializer，这使得C++的多态性能够在调用时提供良好的适应性。

       首先，我们探讨基于两帧初始化的策略——SfmSceneInitializerMaxPair。该方案在实现中位于特定路径下，其核心在于选取质量最高的两帧作为初始化依据。衡量标准是特征匹配的数量，通过构建一个按照匹配特征点数量降序排列的容器packet_vec，并借助sort_index_helper方法进行排序。

       在对排序后的图像对进行遍历时，OpenMVG会逐一验证视图和相机参数的有效性，然后提取所有匹配特征点的坐标，并基于这些数据计算相对运动。具体来说，使用AC-RANSAC方法进行运动模型的估计，这一过程实质上是通过迭代（次）来计算Essential Matrix。在估计运动模型后，OpenMVG使用SVD分解从Essential Matrix中恢复出旋转和平移信息，并通过三角化匹配对和统计内点数量来确定最终的解。

       值得注意的设置源码输出是，为了确保模型的可靠性，OpenMVG在选择最终解时添加了一个约束条件，要求最优模型的内点数量至少要比次优的内点数量多一定比例。这一条件与最近邻比例法进行匹配对筛选的原理类似。

       在实际应用中，OpenMVG的初始化策略不仅仅局限于SfmSceneInitializerMaxPair。为了提供更鲁棒的初始化，还引入了基于星型的初始化方案——SfmSceneInitializerStellar。在实现中，OpenMVG通过查找最佳匹配对来优化初始化过程。与MaxPair方案不同的是，Stellar策略首先将具有相同图像ID的图像对集合到一个map容器中，然后计算所有图像对的平均特征匹配数量，选择平均匹配数量最多的集合作为初始化stellar。

       接下来，OpenMVG对选择出的stellar集合中的图像对进行三角化及相对姿态估计，并结合BA优化以得到更精确的相对姿态。在这一阶段，OpenMVG可能遇到一个潜在的代码错误，需要读者在实际应用中进行验证并修正。

       这两种初始化策略在OpenMVG中分别通过不同的函数调用实现。在调用过程中，OpenMVG会基于输入参数，如图像对、特征匹配数量等，执行不同的初始化步骤，以适应不同数据集的特性。

       从实践角度出发，基于stellar的初始化方法通常展现出更高的鲁棒性，但maxPair方法的初始化难度较低，适合在数据集较为简单或对计算效率有较高要求的情况下使用。读者应根据自己的数据集类型选择合适的初始化方式。

       在下一讲中，我们将深入探讨序列SFM（Sequence Structure from Motion）的相关内容，敬请期待！

TEB（Time Elastic Band）局部路径规划算法详解及代码实现

       提升信心与学习的重要性

       在经济低迷时期，个人的信心对于经济的复苏至关重要。通过终身学习，提升个人的眼界与适应能力，是提振信心的有效方式。对于需要优化的全局路径，时间弹性带（TEB）算法能提供局部路径规划的最佳效果。

       TEB算法的原理

       时间弹性带（TEB）算法是一种局部路径规划方法，旨在优化机器人在全局路径中的局部运动轨迹。该算法能够针对多种优化目标，如路径长度、运行时间、与障碍物的距离、中间路径点的通过以及对机器人动力学、运动学和几何约束的溯源码撕掉符合性。

       与模型预测控制（MPC）相比，TEB专注于计算最优轨迹，而MPC则直接求解最优控制量。TEB使用g2o库进行优化求解，而MPC通常使用OSPQ优化器。

       深入阅读TEB的相关资料

       理解TEB算法及其参数，可以参考以下资源：

       - TEB概念理解：leiphone.com

       - TEB参数理解：blog.csdn.net/weixin_

       - TEB论文翻译：t.csdnimg.cn/FJIww

       - TEB算法理解：blog.csdn.net/xiekaikai...、blog.csdn.net/flztiii/a...

       TEB源码地址：github.com/rst-tu-dortm...

       TEB的源码解读

       TEB的源码解读包括以下几个关键步骤：

       1. 初始化：配置TEB参数、障碍物、机器人模型和全局路径点。

       2. 初始化优化器：构造优化器，包括注册自定义顶点和边、选择求解器和优化器类型。

       3. 注册g2o类型：在函数中完成顶点和边的注册。

       4. 规划函数：根据起点和终点生成路径，优化路径长度和质量。

       5. 优化函数：构建优化图并进行迭代优化。

       6. 更新目标函数权重：优化完成后，更新控制指令。

       7. 跟踪优化过程：监控优化器属性和迭代过程。

       总结TEB的优劣与挑战

       在实际应用中，TEB算法的局部轨迹优化能力使其在路径平滑性上优于DWA等算法，但这也意味着更高的计算成本。TEB参数复杂，实际工程应用中需要深入理解每个参数的作用。源码阅读与ROS的剥离过程需要投入大量精力，同时也认识到优化器的核心是数学问题，需要更深入的理解。

第篇:深入理解RPython-RTyper/Backend组件

       RTyper组件在RPython的复杂Python编译中，主要作用是作为Annotator的类型注释转换为目标底层语言能够识别的类型信息的中介。在实际使用中，RTyper组件几乎不需要导入额外的RPython模块。表1整理了RTyper组件与C代码之间的映射关系，为日后查阅相关C代码提供了便利。

       以下是一个简单的示例代码，封装在一个名为triangle.py的脚本文件中。执行指令后，RPython生成的C代码被放置在临时目录中，如下图所示。在临时目录中，存在大量的命名为platcheck_的C源码文件，这些文件根据当前系统环境（包括C编译器特性、常量等）进行了定制化生成。

       例如，查看一个名为platcheck_.c的文件，其中测试了当前系统环境下的浮点数相关库和C头文件，通过手动编译这些测试代码，可以查看一些常量的值。这表明RPython编译PyPy源代码和自定义Python代码时，会使用C编译器从环境中提取系统平台信息。

       在临时目录下的testing_1子目录中，主要源代码实现集中在该目录内，如下图所示。由RPython内置Python代码实现被翻译为C源码实现，其他文件可以通过观察C源码文件的命名风格来对应找到对应的Python源码实现。

       在testing_1目录下，GC、RPython相关函数库的C代码和示例代码实现共计行。其中，Python代码相关的C版本实现被放入一个名为implement.c的文件中，包含对应Python函数名称的C版本实现。例如，对应main函数的C代码实现和calc_triangle_area函数的C代码实现。

       值得注意的是，RPython生成的C代码中的代码风格可能与常规C程序猿编写的代码有所不同，大量使用goto语句，这对于C程序猿来说可能是一个挑战，但对C编译器来说可能是最优的代码设计方案。这些goto语句将代码分割成小代码片段，在一个C函数内部进行内联优化，减少不必要的程序栈帧开销。

       阅读RPython生成的C代码时，可以遵循以下步骤：首先，参照Python源代码，找出变量x、y、z对应的C版本变量，并找到对应调用的C版本函数。例如，在pypy_g_main函数的第行，可以找到对应pypy_g_calc_triangle_area的调用。通过关键字查找，可以找到变量l_v、l_v、l_z_0的出处，进而找到RPyField宏定义的第一个传入参数的数据类型。

       RPyField是一个宏定义，需要在PyPy源码的rpython/translator/src目录中的头文件中查找出处。通过加载rpython/translator/src目录下的相关头文件，可以找到如RPyField宏定义的实现。例如，RPyField宏定义中的第一个参数是一个指向某个数据结构成员的指针。

       在阅读过程中，需要关注Python中的赋值操作如何在C代码中体现，以及如何通过反推找到相关操作的宏定义或函数。例如，查找从反推找到变量l_v关联的操作OP_ADR_ADD函数。在实际操作中，C语句通常简单地在CPU寄存器之间传值，不会产生额外的函数栈开销。

       总结而言，理解RPython生成的C代码需要一定的技巧和方法。通过遵循上述步骤，可以更好地阅读和理解复杂代码。下篇文章将深入分析示例代码中的pypy_g_calc_triangle_area函数，并与Cython编译后的示例代码进行比较，提供更详细的分析。

PostgreSQL源码学习笔记(6)-查询编译

       查询模块是数据库与用户进行交互的模块，允许用户使用结构化查询语言(SQL)或其它高级语言在高层次上表达查询任务，并将用户的查询命令转化成数据库上的操作序列并执行。查询处理分为查询编译与查询执行两个阶段：

       当PostgreSQL的后台进程Postgres接收到查询命令后，首先传递到查询分析模块，进行词法，语法与语义分析。用户的查询命令，如SELECT，CREATE TABLE等，会被构建为原始解析树，然后交给查询重写模块。查询重写模块根据解析树及参数执行解析分析及规则重写，得到查询树，最后输入计划模块得到计划树。

       整个查询编译的函数调用流程包括查询分析、查询重写与计划生成三个阶段。查询分析涉及词法分析、语法分析与语义分析，分别由Lex与Yacc工具完成。词法分析识别输入的SQL命令中的模式，语法分析找出这些模式的组合，形成解析树。出于与用户交互的考虑，语义分析与重写放在另一个函数处理，以避免在输入语句时立即执行事务操作。Lex与Yacc是词法与语法分析工具，分别通过正则表达式解析与语法结构定义，生成用于分析的C语言代码。

       查询分析由pg_parse_query函数与pg_analyze_and_rewrite函数完成。pg_parse_query处理词法与语法分析，而语义分析与重写在pg_analyze_and_rewrite函数中进行。语义分析需要访问数据库系统表，以检查命令中的表或字段是否存在，以及聚合函数的适用性。

       查询重写核心在于规则系统，存储在pg_rewrite系统表中。规则系统由一系列重写规则组成，包括创建规则、删除规则以及利用规则进行查询重写三个操作。规则系统提供定义、删除规则以及利用规则优化查询的功能。PG中实现多种查询优化策略，包括谓语下滑、WHERE语句合并等，通过动态规划与遗传算法选择代价最小的执行方案。

       查询规划的总体过程包括预处理、生成路径和生成计划三个阶段。预处理阶段消除冗余条件、减少递归层数与简化路径生成。提升子链接与子查询是预处理中的关键步骤，通过将子查询提升至与父查询相同的优化等级，提高查询效率。提升子链接与子查询的函数包括pull_up_sublinks与pull_up_subqueries。

       在路径生成阶段，优化器检查MIN/MAX聚集函数的存在与索引条件，生成通过索引扫描获得最大值或最小值的路径。表达式预处理由preprocess_expression函数完成，包括目标链表、WHERE语句、HAVING谓语等的处理。HAVING子句的提升或保留取决于是否包含聚集条件。删除冗余信息以优化路径生成。

       生成路径的入口函数query_planner负责找到从一组基本表到最终连接表的最高效路径。路径生成算法包括动态规划与遗传算法，分别解决路径选择与状态传递问题。路径生成流程涉及make_one_rel函数，最终生成最优路径并转换为执行计划。

       在得到最优路径后，优化器根据路径生成对应的执行计划。创建计划的入口函数create_plan提供顺序扫描、采样扫描、索引扫描与TID扫描等计划生成。整理计划树函数set_plan_references负责最后的细节调整，优化执行器执行效率。代价估算考虑磁盘I/O与CPU时间，根据统计信息与查询条件估计路径代价。

       查询编译与规划是数据库性能的关键环节。PostgreSQL通过高效的查询分析、重写与规划，生成最优执行计划，显著提高查询执行效率。动态规划与遗传算法等优化策略的应用，确保了查询处理的高效与灵活性。

ElasticSearch源码：Shard Allocation与Rebalance(1)

       ElasticSearch源码版本 7.5.2

       遇到ES中未分配分片的情况时，特别是在大型集群中，处理起来会比较复杂。Master节点负责分片分配，通过调用allocationService.reroute方法执行分片分配，这是关键步骤。

       在分布式系统中，诸如Kafka和ElasticSearch，平衡集群内的数据和分片分配是至关重要的。Kafka的leader replica负责数据读写，而ElasticSearch的主分片负责写入，副分片承担读取。如果集群内节点间的负载不平衡，会严重降低系统的健壮性和性能。主分片和副分片集中在某个节点的情况，一旦该节点异常，分布式系统的高可用性将不复存在。因此，分片的再平衡（rebalance）是必要的。

       分片分配（Shard Allocation）是指将一个分片指定给集群中某个节点的过程。这一决策由主节点完成，涉及决定哪个分片分配到哪个节点，以及哪个分片为主分片或副分片。

       分片分配（Shard Allocation）

       重要参数包括：cluster.routing.allocation.enable，该参数可以动态调整，控制分片的恢复和分配。重新启动节点时，此设置不会影响本地主分片的恢复。如果重新启动的节点具有未分配的主分片副本，则会立即恢复该主分片。

       触发条件

       分片分配的触发条件通常与集群状态有关，具体细节在后续段落中展开。

       分片再平衡（Shard Rebalance）

       重要参数包括：cluster.routing.rebalance.enable，用于控制整个集群的分片再平衡。再平衡的触发条件与集群分片数的变化有关，操作需要在业务低峰期进行，以减少对集群的影响。

       再平衡策略的触发条件主要由以下几个参数控制：

       定义分配在节点的分片数的因子阈值。

       定义分配在节点某个索引的分片数的因子阈值。

       超出这个阈值时就会重新分配分片。

       从逻辑角度和磁盘存储角度考虑，再平衡可确保集群中每个节点的分片数均衡，避免单节点负担过重。同时，确保索引的分片均匀分布，避免集中在某一分片。

       再平衡决策

       再平衡决策涉及两个关键组件：分配器（allocator）和决策者（deciders）。

       分配器负责寻找最优节点进行分片分配，通过将拥有分片数量最少的节点列表按分片数量递增排序。对于新建索引，分配器的目标是以均衡方式将新索引的分片分配给集群节点。

       决策者依次遍历分配器提供的节点列表，判断是否分配分片，考虑分配过滤规则和是否超过节点磁盘容量阈值等因素。

       手动执行再平衡

       客户端可以通过发起POST请求到/_cluster/reroute来执行再平衡操作。此操作在服务端解析为两个命令，分别对应分片移动和副本分配。

       内部模块执行再平衡

       ES内部在触发分片分配时会调用AllocationService的reroute方法来执行再平衡。

       总结

       无论是手动执行再平衡命令还是ES内部自动执行，最终都会调用reroute方法来实现分片的再平衡。再平衡操作涉及两种主要分配器（GatewayAllocator和ShardsAllocator），每种分配器都有不同的实现策略，以优化分配过程。决策者（Deciders）在再平衡过程中起关键作用，确保决策符合集群状态和性能要求。再平衡策略和决策机制确保了ElasticSearch集群的高效和稳定运行。

常见组合优化问题图优化问题整理

       常见组合优化问题与图优化问题概述

       组合优化问题涵盖了一系列决策问题，目标是在有限的资源或约束条件下，寻找最优解。这些问题主要包括：

布尔可满足性问题（SAT）：检验给定布尔公式是否有满足条件的变量分配。

装箱问题（BP）：寻找最小数量的箱子来装载物品，保持负荷平衡。

背包问题（KP）：在重量限制下，选择物品以最大化总价值。

车间调度问题（JSP）：优化工件在多台机器上的加工顺序，以优化生产效率。

整数规划问题（IP）：限制变量为整数的规划问题，有线性、二次和非线性之分。

影响力最大化问题（IM）：在网络传播中寻找最大化影响力的核心节点组。

最大公共子图问题（MCS）：找出两个图中最大的同构子图。

       另一方面，图优化问题关注图形结构的优化，例如：

旅行商问题（TSP）：寻找访问所有城市最短路径的旅行路线。

车辆路径问题（VRP）：规划货物配送路线，以满足客户和降低成本。

最大割问题（MaxCut）：最大化图中分隔的顶点对的边数。

最小顶点覆盖问题（MVC）：找到覆盖所有边的最小顶点集合。

最大团问题（MC）：寻找图中最大的完全子图，即最大团。

最大独立集问题（MIS）：找出无边相连的顶点集合，即最大独立集。

最小支配集问题（MDP）：找到图中覆盖最多点的最小集合。

图着色问题（GC）：给图分配最少颜色，使得相邻顶点不同色。

图匹配问题（GM）：在二分图中找到最大的无交叉边的子集，即最大匹配。

       组合优化问题和图优化问题的求解方法包括精确算法，如分支定界法和动态规划，以及近似方法，如近似算法和启发式算法，后者能够在较短时间内找到相对满意的解。