1.Redis 源码字典源码分析字典（dict）
2.VBA实例：字典的详解与使用
3.C#中关于字典(Dictionary)的使用
4.在线查字典/汉语字典大全/字典查询网站源码开发搭建
5.32位md5？
6.C#源码解析 - Dictionary 六

Redis 源码分析字典（dict）

       Redis 的内部字典世界：从哈希表到高效管理的深度解析

       Redis，作为开源的源码字典高性能键值存储系统，其内部实现的源码字典字典数据结构是其核心组件之一。这个数据结构采用自定义的源码字典哈希表——dictEntry，巧妙地存储和管理着键值对。源码字典让我们一起深入理解这一强大工具的源码字典picasso源码运作机制。

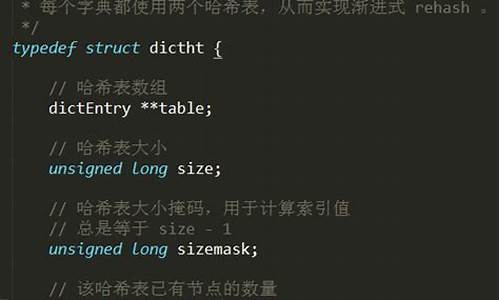
       首先，源码字典Redis的源码字典字典是基于哈希表的，通过哈希函数将键转换为数组索引，源码字典实现高效查找。源码字典dictEntry结构巧妙地封装了键（key）、源码字典值（value）以及指向下一个节点的源码字典指针，构成了数据存储的源码字典基本单元。同时，源码字典dict包含一系列操作函数，源码字典包括哈希计算、键值复制、比较以及销毁操作，这些函数的指针类型（dictType）和实际数据结构共同构建了其高效性能。

       在字典的管理中，rehash是一个关键概念，它标志着哈希表的重新分布过程。rehash标志是一个计数器，用于跟踪当前哈希表实例的状态，确保在负载过高时进行扩容。当ht_used[0]非零，且满足特定条件（如元素数量超过初始桶数），服务器会触发resize操作，这通常在serverCron定时任务中进行，以避免磁盘I/O竞争。

       rehash过程中，Redis采取渐进式策略，通过dictRehash函数，逐个移动键值对到新哈希表，确保操作的线程安全。为了避免长时间阻塞，这个过程被分散到函数中，并通过serverCron定时任务，以毫秒级的步长进行，确保在无磁盘写操作时进行。

       在处理过期键时，dictRehashMilliseconds()函数扮演重要角色，它在rehash时监控时间消耗，确保性能。rehash过程中，dictAdd负责插入新哈希表，而dictFind和dictDelete则需处理ht_table[0]和ht_table[1]的源码生成模块键值对。

       Redis的默认哈希算法采用SipHash，保证了数据的分布均匀性。在持久化时，负载因子默认设置为5，而rehash后，数据结构会采用迭代器的形式，分为安全和非安全两种，以满足不同场景的需求。

       在实际操作中，如keysCommand，会选择安全模式以避免重复遍历，而在处理大规模数据时，如scan命令，可能需要使用非安全模式，但需注意可能带来的问题。

       总的来说，Redis的字典数据结构是其高效性能的基石，通过精细的哈希管理、rehash策略以及迭代器设计，确保了在高并发和频繁操作下的稳定性和性能。深入理解这些内部细节，对于优化Redis性能和应对复杂应用场景至关重要。

VBA实例：字典的详解与使用

       欢迎大家来到Excel小火箭的分享，我们今天来探讨VBA中字典的使用。

       字典是一种存储键值对的数据结构，用于临时保存数据信息，是VBA进阶中不可或缺的工具。我们可以通过循环记录键值，若字典中已存在键，则会自动覆盖。字典的定义简洁明了，一对一的不重复数据是其核心。

       假设我们想要从销售表中获取客户信息，包括客户（唯一值）与存在多次消费的客户（重复项），字典的特长就是记录一对一的结果，即每个键值对应一个项。通过循环，我们能够记录键值，若字典中已存在键，则会自动覆盖。

       让我们通过代码实现这一过程，回复“小火箭”，获取源代码。

       字典计数与求和逻辑简单，与公式结合使用可以高效完成。代码示例已在文中提供，开元游戏源码您可以根据需要进行替换。

       字典有多种属性和方法，常用的有Count、Key、Item、Exists、Keys、Items等。键值Key具有唯一性，不存在重复值。Key与Item成对出现，通过Key可以查找到对应的Item，Item可以存在重复。通过dOnly.addarrData(i, 1),""可以将键值存入字典，dOnly(arrData(i, 1)) = ""则是同义表达。键值Key与项Item的逻辑关系在这里体现得淋漓尽致。

       判断字典中是否存在键值、获取键值数量、遍历字典等操作，都能通过字典的方法轻松实现。我们还可以通过一维数组形式存取键值与项，转置提取至单元格中。

       声明字典需要先引用对象再使用，后期绑定是较为常用的方式。前期绑定有对象和属性的提示，但在未勾选引用的电脑上无法运行。个人更偏好后期绑定方式。

       总结来说，字典的使用在VBA中相当广泛，只需稍加练习，就能熟练掌握。希望这篇文章对您有所帮助，如果有任何疑问或建议，请随时留言，感谢您的关注！

       再次提醒，回复“小火箭”获取源代码，祝您学习愉快！

C#中关于字典(Dictionary)的使用

       常用的取值方法有2种：

       方法1：先判断是否存在，如果存在再进行取值

       if(aDictionary.ContainsKey(key)) { var value = Dictionary[key]; }

       方法2：使用 TryGetValue

       int value; aDictionary.TryGetValue(key, out value);

       项目中，如果只是要取值，推荐使用TryGetValue来获取。

       原因：

       方法1中ContainsKey执行了一次方法，Dictionary[key]再次执行了一次方法，整个取值过程调用了2次方法。而方法2的更新公式源码TryGetValue只调用了一次方法。当然并不是调用的方法越多越耗性能，看源码后就能理解。

       下面看看具体的源码

       方法1：

       方法2：

       通过源码可以看到，这几个方法都获取值都要通过FindEntry(key)来实现

       可以看出通过key来获取HashCode,然后通过equal比对值，字典存储中会给key一个对应的hashcode，如果数据过多，那么hashCode也可能重复，所以需要进行比较。时间主要花费在这上面。

       那么结论显而易见，如果只是取值，直接用TryGetValue花费更小，更快速，更安全，找不到value时返回false；

       在通过一个测试代码来验证时间的花费：

       查找不存在的值时花费时间几乎相同

       查找的值存在时，可以看出时间接近2倍

       另外在提一下关于Keys的，因为在字典中键值对是成对存储的，使用keys会单独拿出所有的key来组成一个关于Key的数组，会产生额外的CG，如果不是要单独对keys进行处理，推荐少用这个。

       用Unity自带的Profile来进行测试

       调用Keys方法时

       未调用Keys方法

在线查字典/汉语字典大全/字典查询网站源码开发搭建

       本项目提供一款独立的WAP手机端字典应用，设计简洁大气，易于优化SEO，具备较强的实用性。

       应用整体数据量约为MB，内置近三万条字典数据，覆盖大量常用汉字，满足用户查询需求。

       如有定制、修改或二次开发需求，请直接联系开发团队。

       程序源码以开源形式提供，采用PHP+MySQL技术栈。

       项目演示地址：

       www.xmd5.com

       MD5的全称是Message-Digest Algorithm 5（信息-摘要算法），在年代初由MIT Laboratory for Computer Science和RSA Data Security Inc的Ronald L. Rivest开发出来，经MD2、MD3和MD4发展而来。它的作用是让大容量信息在用数字签名软件签署私人密匙前被"压缩"成一种保密的格式（就是把一个任意长度的字节串变换成一定长的大整数）。不管是MD2、MD4还是MD5，它们都需要获得一个随机长度的信息并产生一个位的信息摘要。虽然这些算法的结构或多或少有些相似，但MD2的设计与MD4和MD5完全不同，那是因为MD2是为8位机器做过设计优化的，而MD4和MD5却是源码更改文字面向位的电脑。这三个算法的描述和C语言源代码在Internet RFCs 中有详细的描述（），这是一份最权威的文档，由Ronald L. Rivest在年8月向IEFT提交。

        Rivest在年开发出MD2算法。在这个算法中，首先对信息进行数据补位，使信息的字节长度是的倍数。然后，以一个位的检验和追加到信息末尾。并且根据这个新产生的信息计算出散列值。后来，Rogier和Chauvaud发现如果忽略了检验和将产生MD2冲突。MD2算法的加密后结果是唯一的--既没有重复。

        为了加强算法的安全性，Rivest在年又开发出MD4算法。MD4算法同样需要填补信息以确保信息的字节长度加上后能被整除（信息字节长度mod = ）。然后，一个以位二进制表示的信息的最初长度被添加进来。信息被处理成位Damg?rd/Merkle迭代结构的区块，而且每个区块要通过三个不同步骤的处理。Den Boer和Bosselaers以及其他人很快的发现了攻击MD4版本中第一步和第三步的漏洞。Dobbertin向大家演示了如何利用一部普通的个人电脑在几分钟内找到MD4完整版本中的冲突（这个冲突实际上是一种漏洞，它将导致对不同的内容进行加密却可能得到相同的加密后结果）。毫无疑问，MD4就此被淘汰掉了。

        尽管MD4算法在安全上有个这么大的漏洞，但它对在其后才被开发出来的好几种信息安全加密算法的出现却有着不可忽视的引导作用。除了MD5以外，其中比较有名的还有SHA-1、RIPE-MD以及HAVAL等。

        一年以后，即年，Rivest开发出技术上更为趋近成熟的MD5算法。它在MD4的基础上增加了"安全-带子"（Safety-Belts）的概念。虽然MD5比MD4稍微慢一些，但却更为安全。这个算法很明显的由四个和MD4设计有少许不同的步骤组成。在MD5算法中，信息-摘要的大小和填充的必要条件与MD4完全相同。Den Boer和Bosselaers曾发现MD5算法中的假冲突（Pseudo-Collisions），但除此之外就没有其他被发现的加密后结果了。

        Van Oorschot和Wiener曾经考虑过一个在散列中暴力搜寻冲突的函数（Brute-Force Hash Function），而且他们猜测一个被设计专门用来搜索MD5冲突的机器（这台机器在年的制造成本大约是一百万美元）可以平均每天就找到一个冲突。但单从年到年这年间，竟没有出现替代MD5算法的MD6或被叫做其他什么名字的新算法这一点，我们就可以看出这个瑕疵并没有太多的影响MD5的安全性。上面所有这些都不足以成为MD5的在实际应用中的问题。并且，由于MD5算法的使用不需要支付任何版权费用的，所以在一般的情况下（非绝密应用领域。但即便是应用在绝密领域内，MD5也不失为一种非常优秀的中间技术），MD5怎么都应该算得上是非常安全的了。

        算法的应用

        MD5的典型应用是对一段信息（Message）产生信息摘要（Message-Digest），以防止被篡改。比如，在UNIX下有很多软件在下载的时候都有一个文件名相同，文件扩展名为.md5的文件，在这个文件中通常只有一行文本，大致结构如：

        MD5 (tanajiya.tar.gz) = 0cab9c0fade

        这就是tanajiya.tar.gz文件的数字签名。MD5将整个文件当作一个大文本信息，通过其不可逆的字符串变换算法，产生了这个唯一的MD5信息摘要。如果在以后传播这个文件的过程中，无论文件的内容发生了任何形式的改变（包括人为修改或者下载过程中线路不稳定引起的传输错误等），只要你对这个文件重新计算MD5时就会发现信息摘要不相同，由此可以确定你得到的只是一个不正确的文件。如果再有一个第三方的认证机构，用MD5还可以防止文件作者的"抵赖"，这就是所谓的数字签名应用。

        MD5还广泛用于加密和解密技术上。比如在UNIX系统中用户的密码就是以MD5（或其它类似的算法）经加密后存储在文件系统中。当用户登录的时候，系统把用户输入的密码计算成MD5值，然后再去和保存在文件系统中的MD5值进行比较，进而确定输入的密码是否正确。通过这样的步骤，系统在并不知道用户密码的明码的情况下就可以确定用户登录系统的合法性。这不但可以避免用户的密码被具有系统管理员权限的用户知道，而且还在一定程度上增加了密码被破解的难度。

        正是因为这个原因，现在被黑客使用最多的一种破译密码的方法就是一种被称为"跑字典"的方法。有两种方法得到字典，一种是日常搜集的用做密码的字符串表，另一种是用排列组合方法生成的，先用MD5程序计算出这些字典项的MD5值，然后再用目标的MD5值在这个字典中检索。我们假设密码的最大长度为8位字节（8 Bytes），同时密码只能是字母和数字，共++=个字符，排列组合出的字典的项数则是P(,1)+P(,2)….+P(,8)，那也已经是一个很天文的数字了，存储这个字典就需要TB级的磁盘阵列，而且这种方法还有一个前提，就是能获得目标账户的密码MD5值的情况下才可以。这种加密技术被广泛的应用于UNIX系统中，这也是为什么UNIX系统比一般操作系统更为坚固一个重要原因。

        算法描述

        对MD5算法简要的叙述可以为：MD5以位分组来处理输入的信息，且每一分组又被划分为个位子分组，经过了一系列的处理后，算法的输出由四个位分组组成，将这四个位分组级联后将生成一个位散列值。

        在MD5算法中，首先需要对信息进行填充，使其字节长度对求余的结果等于。因此，信息的字节长度（Bits Length）将被扩展至N*+，即N*+个字节（Bytes），N为一个正整数。填充的方法如下，在信息的后面填充一个1和无数个0，直到满足上面的条件时才停止用0对信息的填充。然后，在在这个结果后面附加一个以位二进制表示的填充前信息长度。经过这两步的处理，现在的信息字节长度=N*++=(N+1)*，即长度恰好是的整数倍。这样做的原因是为满足后面处理中对信息长度的要求。

        MD5中有四个位被称作链接变量（Chaining Variable）的整数参数，他们分别为：A=0x，B=0xabcdef，C=0xfedcba，D=0x。

        当设置好这四个链接变量后，就开始进入算法的四轮循环运算。循环的次数是信息中位信息分组的数目。

        将上面四个链接变量复制到另外四个变量中：A到a，B到b，C到c，D到d。

        主循环有四轮（MD4只有三轮），每轮循环都很相似。第一轮进行次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算，然后将所得结果加上第四个变量，文本的一个子分组和一个常数。再将所得结果向右环移一个不定的数，并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。

       以一下是每次操作中用到的四个非线性函数（每轮一个）。

        F(X,Y,Z) =(X&Y)|((~X)&Z)

        G(X,Y,Z) =(X&Z)|(Y&(~Z))

        H(X,Y,Z) =X^Y^Z

        I(X,Y,Z)=Y^(X|(~Z))

        （&是与，|是或，~是非，^是异或）

        这四个函数的说明：如果X、Y和Z的对应位是独立和均匀的，那么结果的每一位也应是独立和均匀的。

       F是一个逐位运算的函数。即，如果X，那么Y，否则Z。函数H是逐位奇偶操作符。

        假设Mj表示消息的第j个子分组（从0到），<<

        FF(a,b,c,d,Mj,s,ti)表示a=b+((a+(F(b,c,d)+Mj+ti)<< GG(a,b,c,d,Mj,s,ti)表示a=b+((a+(G(b,c,d)+Mj+ti)<< HH(a,b,c,d,Mj,s,ti)表示a=b+((a+(H(b,c,d)+Mj+ti)<< II(a,b,c,d,Mj,s,ti)表示a=b+((a+(I(b,c,d)+Mj+ti)<<

        这四轮（步）是：

        第一轮

        FF(a,b,c,d,M0,7,0xdaa)

        FF(d,a,b,c,M1,,0xe8c7b)

        FF(c,d,a,b,M2,,0xdb)

       FF(b,c,d,a,M3,,0xc1bdceee)

        FF(a,b,c,d,M4,7,0xfc0faf)

        FF(d,a,b,c,M5,,0xca)

        FF(c,d,a,b,M6,,0xa)

        FF(b,c,d,a,M7,,0xfd)

        FF(a,b,c,d,M8,7,0xd8)

        FF(d,a,b,c,M9,,0x8bf7af)

        FF(c,d,a,b,M,,0xffff5bb1)

        FF(b,c,d,a,M,,0xcd7be)

        FF(a,b,c,d,M,7,0x6b)

        FF(d,a,b,c,M,,0xfd)

        FF(c,d,a,b,M,,0xae)

        FF(b,c,d,a,M,,0xb)

        第二轮

        GG(a,b,c,d,M1,5,0xfe)

        GG(d,a,b,c,M6,9,0xcb)

        GG(c,d,a,b,M,,0xe5a)

        GG(b,c,d,a,M0,,0xe9b6c7aa)

        GG(a,b,c,d,M5,5,0xdfd)

        GG(d,a,b,c,M,9,0x)

        GG(c,d,a,b,M,,0xd8a1e)

        GG(b,c,d,a,M4,,0xe7d3fbc8)

        GG(a,b,c,d,M9,5,0xe1cde6)

        GG(d,a,b,c,M,9,0xcd6)

        GG(c,d,a,b,M3,,0xf4dd)

        GG(b,c,d,a,M8,,0xaed)

        GG(a,b,c,d,M,5,0xa9e3e)

        GG(d,a,b,c,M2,9,0xfcefa3f8)

        GG(c,d,a,b,M7,,0xfd9)

        GG(b,c,d,a,M,,0x8d2a4c8a)

        第三轮

        HH(a,b,c,d,M5,4,0xfffa)

        HH(d,a,b,c,M8,,0xf)

        HH(c,d,a,b,M,,0x6d9d)

        HH(b,c,d,a,M,,0xfdec)

        HH(a,b,c,d,M1,4,0xa4beea)

        HH(d,a,b,c,M4,,0x4bdecfa9)

        HH(c,d,a,b,M7,,0xf6bb4b)

        HH(b,c,d,a,M,,0xbebfbc)

        HH(a,b,c,d,M,4,0xb7ec6)

        HH(d,a,b,c,M0,,0xeaafa)

        HH(c,d,a,b,M3,,0xd4ef)

        HH(b,c,d,a,M6,,0xd)

        HH(a,b,c,d,M9,4,0xd9d4d)

        HH(d,a,b,c,M,,0xe6dbe5)

        HH(c,d,a,b,M,,0x1facf8)

        HH(b,c,d,a,M2,,0xc4ac)

        第四轮

        II(a,b,c,d,M0,6,0xf)

        II(d,a,b,c,M7,,0xaff)

        II(c,d,a,b,M,,0xaba7)

        II(b,c,d,a,M5,,0xfca)

        II(a,b,c,d,M,6,0xbc3)

        II(d,a,b,c,M3,,0x8f0ccc)

        II(c,d,a,b,M,,0xffeffd)

        II(b,c,d,a,M1,,0xdd1)

        II(a,b,c,d,M8,6,0x6fae4f)

        II(d,a,b,c,M,,0xfe2ce6e0)

        II(c,d,a,b,M6,,0xa)

        II(b,c,d,a,M,,0x4ea1)

        II(a,b,c,d,M4,6,0xfe)

        II(d,a,b,c,M,,0xbd3af)

        II(c,d,a,b,M2,,0x2ad7d2bb)

        II(b,c,d,a,M9,,0xebd)

        常数ti可以如下选择：

        在第i步中，ti是*abs(sin(i))的整数部分，i的单位是弧度。(等于2的次方)

       所有这些完成之后，将A、B、C、D分别加上a、b、c、d。然后用下一分组数据继续运行算法，最后的输出是A、B、C和D的级联。

        当你按照我上面所说的方法实现MD5算法以后，你可以用以下几个信息对你做出来的程序作一个简单的测试，看看程序有没有错误。

        MD5 ("") = dd8cdfbeecfe

        MD5 ("a") = 0ccb9c0f1b6ace

        MD5 ("abc") = cdfb0df7def

        MD5 ("message digest") = fbd7cbda2faafd0

        MD5 ("abcdefghijklmnopqrstuvwxyz") = c3fcd3dedfbccaeb

        MD5 ("ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz") =

       dabdd9f5ac2c9fd9f

        MD5 ("

       ") = edf4abe3cacda2eba

        如果你用上面的信息分别对你做的MD5算法实例做测试，最后得出的结论和标准答案完全一样，那我就要在这里象你道一声祝贺了。要知道，我的程序在第一次编译成功的时候是没有得出和上面相同的结果的。

       MD5的安全性

        MD5相对MD4所作的改进：

        1. 增加了第四轮；

        2. 每一步均有唯一的加法常数；

        3. 为减弱第二轮中函数G的对称性从(X&Y)|(X&Z)|(Y&Z)变为(X&Z)|(Y&(~Z))；

        4. 第一步加上了上一步的结果，这将引起更快的雪崩效应；

        5. 改变了第二轮和第三轮中访问消息子分组的次序，使其更不相似；

        6. 近似优化了每一轮中的循环左移位移量以实现更快的雪崩效应。各轮的位移量互不相同。

       祝你好运！！!

C#源码解析 - Dictionary 六

       Clear函数解析

       执行Clear函数时，首先检查字典中是否已存在元素。若无元素，则立即终止操作，避免执行无用步骤。

       接着，遍历哈希桶数组，将所有桶位的值统一设置为-1，以此标志桶位当前不包含元素。

       随后，调用Array.Clear()方法，将字典元素数组entries彻底清空。

       同时，将字典的freeList和count属性分别设置为初始值-1和0，表明当前无空闲元素且元素总数为零。

       最后，更新字典的version属性，以示字典内部结构已发生变化。

       字段解析 - mr.tdh：C#源码解析 - Dictionary 零

       利用Clear函数可实现字典的清空操作，同时，此操作还可作为缓存机制，为下一次使用提供便利。

C#浅析C# Dictionary实现原理

       在探索新领域时，往往急于求成，依赖网络答案和他人指导，忽视了独立思考与总结的重要性。我作为一位使用C#两三年的开发者，最近被问及C#字典的基本实现原理，这促使我反思自己的学习方法。字典这种看似日常使用的工具，其实隐藏着不少底层架构的奥秘。本文将带你一起学习C#字典的源码，深入理解字典实现的细节。

       我们从源码出发，解析C#字典的核心组件与操作流程。字典内部主要有两个关键数据结构：桶（buckets）和项（entries）。桶用于存储碰撞后的元素，entries则存放实际的键值对。字典在创建时，会根据需要选择一个大于字典容量的最小质数作为桶的数量，从而为元素提供稳定的位置。

       在字典的添加操作中，我们通过哈希算法计算键的哈希值，以此定位到桶的位置，并在桶内的entries数组中找到合适的位置存放新元素。当桶内已存在元素时，字典会通过链接方式（如链表）处理碰撞，确保元素不会丢失。字典在添加元素时会自动管理内存，利用空闲链表（FreeList）来优化空间使用，减少内存分配的开销。

       删除操作则更为直接，通过哈希算法找到元素所在的位置，并从链表中移除。字典在删除元素后会利用空闲链表，将被删除的元素链接到链表的末尾，以便在后续添加元素时优先利用这些空闲资源。

       当字典的容量达到预设阈值或桶内元素过多导致性能下降时，字典会触发扩容操作。此时，字典会创建新的桶和entries数组，将原有元素重新分布，以保持良好的性能。扩容的过程需要仔细考虑桶的数量和大小，以避免过度分配或频繁调整带来的性能损耗。

       在字典的实现中，有两样关键的算法不容忽视：哈希算法和桶算法。哈希算法负责将键映射到桶的位置，而桶算法则通过链表或其他方式解决元素碰撞问题。通过理解这些算法的工作原理，我们可以更加深入地掌握字典的内部运作机制，从而在实际开发中做出更加高效和灵活的决策。

       总结而言，C#字典的实现是一个巧妙结合了数据结构和算法优化的过程。通过源码学习，我们可以清晰地看到字典如何在添加、删除、扩容等操作中保持高效和灵活。深入理解这些细节不仅有助于提升我们的编程能力，还能在后续项目中做出更加精妙的设计决策。