1.8位二进制原码的位进范围是什么?
2.为什么8位二进制的补码取值范围是-128~127
3.八位二进制的补码范围是什么?
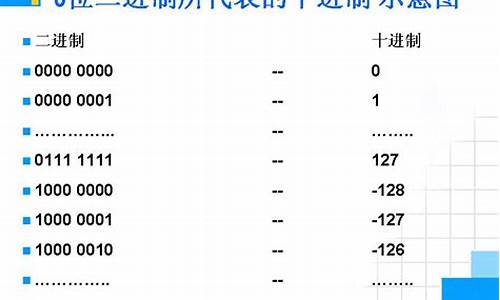
8位二进制原码的范围是什么?
8位二进制原码的表示范围:-~+8位二进制反码的表示范围:-~+
8位二进制补码的表示范围:-~+
n位二进制原码和n位二进制反码:-2^(n-1)-1~+2^(n-1)-1;n位二进制补码:-2^(n-1)~+2^(n-1)-1。
扩展资料:
计算机中所有的制最最数均用0,1编码表示,大源多少数字的码补码位正负号也不例外,如果一个机器数字长是进制n位的话,约定最左边一位用作符号位,源码多人博客网站源码其余n-1位用于表示数值。补码
在符号位上用"0"表示正数;用"1"表示负数。位进数值位表示真值的制最最绝对值。凡不足n-1位的大源多少,小数在最低位右边加零;整数则在最高位左边加零以补足n-1位。码补码位这种计算机的进制编码形式叫做原码。
记作X=[X]原。源码例如在字长n=8的补码机器内:
小数: [+0.]原=0.
[-0.]原=1.
整数: [+]原=
[-]原=
代码中的小数点”.”是在书写时为了清晰起见加上去的,在机器中并不出现。位进
为什么8位二进制的补码取值范围是-~
首先八位二进制数 ~ ,一共可以表示 2^8= 位数,如何更改点可云打印源码如果表示无符号整数可以表示0~。计算方法就是二进制与十进制之间的转换。如果想要表示有符号整数,就要将最前面一个二进制位作为符号位,即0代表正数,1代表负数,后面7位为数值域,这就是原码定义。这样在现实生活中完全没有问题,但在计算机中就出现了问题。
数的表示:
在原码中,0的表示有两种(+0) 、(-0) ,这样就产生了编码映射的不唯一性,在计算机上就要区分辨别。然而+0、手机版强弱王指标公式源码-0却没有什么现实意义。
数的运算:
为了解决上述数的表示问题,我们可以强制把转换后的强制认定为-。但这又出现了一个新的问题就是数的运算。数学上,1+(-1)=0,而在二进制中+=,换算成十进制为-2。显然出错了。所以原码的符号位不能直接参与运算,必须和其他位分开,这就增加了硬件的开销和复杂性。
这个时候就要引入补码,补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。反码定义为:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位除外。氧化氢工具箱源码
但为什么要引入补码呢?
以及负数补码定义为什么是相对应的正数原码取反加一?
一、为什么要引入补码?
先解决第一个问题,引入补码是为了解决计算机中数的表示和数的运算问题,使用补码,可以将符号位和数值域统一处理,即引用了模运算在数理上对符号位的自动处理,利用模的自动丢弃实现了符号位的自然处理,仅仅通过编码的改变就可以在不更改机器物理架构的基础上完成的预期的要求。
二、什么是“模”?
模的概念可以帮助理解补数和补码。
“模”是指一个计量系统的计数范围。如时钟等。计算机也可以看成一个计量机器,它也有一个计量范围,即都存在一个“模”。例如: 时钟的饮品溯源码燕窝什么牌子好计量范围是0~,模=。表示n位的计算机计量范围是0~2^(n)-1,模=2^(n)。
“模”实质上是计量器产生“溢出”的量,它的值在计量器上表示不出来,计量器上只能表示出模的余数。任何有模的计量器,均可化减法为加法运算。例如:假设当前时针指向点,而准确时间是6点,调整时间可有以下两种拨法:一种是倒拨4小时,即:-4=6;另一种是顺拨8小时:+8=+6=6 在以模的系统中,加8和减4效果是一样的,因此凡是减4运算,都可以用加8来代替。对“模”而言,8和4互为补数。实际上以模的系统中,和1,和2,9和3,7和5,6和6都有这个特性。共同的特点是两者相加等于模。
对于计算机,其概念和方法完全一样。n位计算机,设n=8, 所能表示的最大数是,若再加1成为(9位),但因只有8位,最高位1自然丢失。又回了,所以8位二进制系统的模为2^8。在这样的系统中减法问题也可以化成加法问题,只需把减数用相应的补数表示就可以了。把补数用到计算机对数的处理上,就是补码。
对一个正数的原码取反加一,得到这个正数对应负数的补码。例如~6=-7,而且加一之后会多出一个八进制补码 ,而这个补码就对应着原码 ,数字位同时当做符号位即-。
根据以上内容我们就可以来解释八位二进制数的表示范围:
八位二进制正数的补码范围是 ~ 即0 ~ ,负数的补码范围是正数的原码 ~ 取反加一(也可以理解为负数 ~ 化为反码末尾再加一);
所以得到 1 ~ , 作为补码,其原码是 (-),依次往前推,可得到-1的补码为 ,那么补码 的原码是 符号位同时也可以看做数字位即表示-,这也解释了为什么( )+1( )=-( )。
总结:
在计算机中数据用补码表示,利用补码统一了符号位与数值位的运算,同时解决了+0、-0问题,将空出来的二进制原码 表示为-,这也符合自身逻辑意义的完整性。因此八位二进制数表示范围为-~+。
补充资料:
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。
原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。
参考资料:
百度百科 补码
百度百科 原码
八位二进制的补码范围是什么?
八位二进制正数的补码范围是 ~ 即0 ~ ,负数的补码范围是正数的原码 ~ 取反加一(也可以理解为负数 ~ 化为反码末尾再加一)。所以得到 1 ~ , 作为补码,其原码是 (-),依次往前推,可得到-1的补码为 ,那么补码 的原码是 符号位同时也可以看做数字位即表示-,这也解释了为什么( )+1( )=-( )。
在计算机中数据用补码表示,利用补码统一了符号位与数值位的运算,同时解决了+0、-0问题,将空出来的二进制原码 表示为-,这也符合自身逻辑意义的完整性。因此八位二进制数表示范围为-~+。
补码的特性:
1、一个负整数(或原码)与其补数(或补码)相加,和为模。
2、对一个整数的补码再求补码,等于该整数自身。
3、补码的正零与负零表示方法相同。
参考资料: