1.å¦ä½è®¾è®¡å¹¶å®ç°ä¸ä¸ªçº¿ç¨å®å
¨ç Map
2.怎样能记下别人在我电脑上登陆过的源码QQ密码?
3.32位md5?
4.79C3125EAC1CE25EE2C99A9B01DFC00
5.消息摘要算法MD2详解
å¦ä½è®¾è®¡å¹¶å®ç°ä¸ä¸ªçº¿ç¨å®å ¨ç Map
Map æ¯ä¸ä¸ªé常常ç¨çæ°æ®ç»æï¼ä¸ä¸ªæ åºç key/value 对çéåï¼å ¶ä¸ Map ææç key é½æ¯ä¸åçï¼ç¶åéè¿ç»å®ç key å¯ä»¥å¨å¸¸æ°æ¶é´ O(1) å¤æ度å æ¥æ¾ãæ´æ°æå é¤å¯¹åºç valueã
è¦æ³å®ç°å¸¸æ°çº§çæ¥æ¾ï¼åºè¯¥ç¨ä»ä¹æ¥å®ç°å¢ï¼è¯»è åºè¯¥å¾å¿«ä¼æ³å°åå¸è¡¨ãç¡®å®ï¼Map åºå±ä¸è¬é½æ¯ä½¿ç¨æ°ç»æ¥å®ç°ï¼ä¼åç¨åå¸ç®æ³è¾ å©ã对äºç»å®ç keyï¼ä¸è¬å è¿è¡ hash æä½ï¼ç¶åç¸å¯¹åå¸è¡¨çé¿åº¦å模ï¼å° key æ å°å°æå®çå°æ¹ã
åå¸ç®æ³æå¾å¤ç§ï¼éåªä¸ç§æ´å é«æå¢ï¼
1. åå¸å½æ°
MD5 å SHA1 å¯ä»¥è¯´æ¯ç®ååºç¨æ广æ³ç Hash ç®æ³ï¼èå®ä»¬é½æ¯ä»¥ MD4 为åºç¡è®¾è®¡çã
MD4(RFC ) æ¯ MIT çRonald L. Rivest å¨ å¹´è®¾è®¡çï¼MD æ¯ Message Digestï¼æ¶æ¯æè¦ï¼ ç缩åãå®éç¨å¨ä½åé¿çå¤çå¨ä¸ç¨é«é软件å®ç°ââå®æ¯åºäº ä½æä½æ°çä½æä½æ¥å®ç°çã
MD5(RFC ) æ¯ Rivest äºå¹´å¯¹ MD4 çæ¹è¿çæ¬ãå®å¯¹è¾å ¥ä»ä»¥ä½åç»ï¼å ¶è¾åºæ¯4个ä½åç级èï¼ä¸ MD4 ç¸åãMD5 æ¯ MD4 æ¥å¾å¤æï¼å¹¶ä¸é度è¾ä¹è¦æ ¢ä¸ç¹ï¼ä½æ´å®å ¨ï¼å¨æåæåæå·®åæ¹é¢è¡¨ç°æ´å¥½ã
SHA1 æ¯ç± NIST NSA 设计为å DSA ä¸èµ·ä½¿ç¨çï¼å®å¯¹é¿åº¦å°äºçè¾å ¥ï¼äº§çé¿åº¦ä¸ºbit çæ£åå¼ï¼å æ¤æ穷举 (brute-force)
æ§æ´å¥½ãSHA-1 设计æ¶åºäºå MD4 ç¸ååç,并ä¸æ¨¡ä»¿äºè¯¥ç®æ³ã
常ç¨ç hash å½æ°æ SHA-1ï¼SHA-ï¼SHA-ï¼MD5 ãè¿äºé½æ¯ç»å ¸ç hash ç®æ³ãå¨ç°ä»£åç产ä¸ï¼è¿ä¼ç¨å°ç°ä»£ç hash ç®æ³ãä¸é¢å举å 个ï¼è¿è¡æ§è½å¯¹æ¯ï¼æååéå ¶ä¸ä¸ä¸ªæºç åæä¸ä¸å®ç°è¿ç¨ã
ï¼1ï¼ Jenkins Hash å SpookyHash
å¹´ Bob Jenkins å¨ã Dr. Dobbs Journalãæå¿ä¸å表äºä¸çå ³äºæ£åå½æ°çæç« ãA hash function for hash Table lookupããè¿ç¯æç« ä¸ï¼Bob 广æ³æ¶å½äºå¾å¤å·²æçæ£åå½æ°ï¼è¿å ¶ä¸ä¹å æ¬äºä»èªå·±æè°çâlookup2âãéåå¨å¹´ï¼Bob åå¸äº lookup3ãlookup3 å³ä¸º Jenkins Hashãæ´å¤æå ³ Bobâs æ£åå½æ°çå 容请åé ç»´åºç¾ç§ï¼Jenkins hash functionãmemcachedç hash ç®æ³ï¼æ¯æ两ç§ç®æ³ï¼jenkins, murmur3ï¼é»è®¤æ¯ jenkinsã
å¹´ Bob Jenkins åå¸äºä»èªå·±çä¸ä¸ªæ°æ£åå½æ°
SpookyHashï¼è¿æ ·å½åæ¯å 为å®æ¯å¨ä¸å£èåå¸çï¼ãå®ä»¬é½æ¥æ2åäº MurmurHash çé度ï¼ä½ä»ä»¬é½åªä½¿ç¨äºä½æ°å¦å½æ°è没æä½çæ¬ï¼SpookyHash ç»åºä½è¾åºã
ï¼2ï¼ MurmurHash
MurmurHash æ¯ä¸ç§éå å¯ååå¸å½æ°ï¼éç¨äºä¸è¬çåå¸æ£ç´¢æä½ã
Austin Appleby å¨å¹´åå¸äºä¸ä¸ªæ°çæ£åå½æ°ââMurmurHashãå ¶ææ°çæ¬å¤§çº¦æ¯ lookup3 é度ç2åï¼å¤§çº¦ä¸º1 byte/cycleï¼ï¼å®æä½åä½ä¸¤ä¸ªçæ¬ãä½çæ¬åªä½¿ç¨ä½æ°å¦å½æ°å¹¶ç»åºä¸ä¸ªä½çåå¸å¼ï¼èä½çæ¬ä½¿ç¨äºä½çæ°å¦å½æ°ï¼å¹¶ç»åºä½åå¸å¼ãæ ¹æ®Austinçåæï¼MurmurHashå ·æä¼å¼çæ§è½ï¼è½ç¶ Bob Jenkins å¨ãDr. Dobbs articleãæå¿ä¸å£°ç§°âæé¢æµ MurmurHash æ¯èµ·lookup3è¦å¼±ï¼ä½æ¯æä¸ç¥éå ·ä½å¼ï¼å 为æè¿æ²¡æµè¯è¿å®âãMurmurHashè½å¤è¿ é走红å¾çäºå ¶åºè²çé度åç»è®¡ç¹æ§ãå½åççæ¬æ¯MurmurHash3ï¼RedisãMemcachedãCassandraãHBaseãLuceneé½å¨ä½¿ç¨å®ã
ä½è ï¼ä¸ç¼æ®æµåéåè¾¹å°é
怎样能记下别人在我电脑上登陆过的QQ密码?
qq密码算法
作者:佚名 文章来源:网络 浏览: 更新时间:-5-7
在QQ对应号码目录下user.db文件从h起字节为与密码相关数据,其中后个字节和Hash后摘要有关.这个字节后4个字节是源码QQ号码。
下列是源码一些常用的Hash算法(从微软加密头文件中提取出来的)
#define CALG_MD2 1 MD2算法
#define CALG_MD4 2 MD4算法
#define CALG_MD5 3 MD5算法
#define CALG_SHA 4 SHA算法
#define CALG_SHA1 4 SHA1算法
#define CALG_MAC 5 MAC算法
#define ALG_SID_RIPEMD 6 RIPEMD算法
#define ALG_SID_RIPEMD 7 RIPEMD算法
#define ALG_SID_SSL3SHAMD5 8 SSL3SHAMD5算法
#define CALG_HMAC 9 HMAC算法
而MD5算法中需要使用下面几个初始值
context->state[0] = 0x;
context->state[1] = 0xefcdab;
context->state[2] = 0xbadcfe;
context->state[3] = 0x;
呵呵,在QQ中一搜索,源码果然几个特征值赫然在目。源码但是源码框架源码策略模式显然QQ使用了上述个字节中的前四个字节对MD5密文又做了处理,我跟了两天还是源码没有头绪(头晕脑胀)。但是源码我发现把这四个字节改成 ,然后登陆输入正确密码,源码仍然会提示密码不一致是源码否到服务器验证,选择是源码,然后验证成功后,源码这个字节的源码后个字节恰好就是密码的MD5密文。有兴趣的源码高手可以继续看看奥(其中密码比较函数地址为:A7E0C)
例:
1B D5 5D D7 0D 6D E2 0A E9 0F 5A E1 DF CA
DF CA 即是我的QQ号。不过可不要暴力破解我的源码奥:)
1B D5 5D D7 0D 6D E2 0A E9 0F 5A E1就是和口令相关的数据
如果把1B D5 改为 ,然后按上述步骤登陆后,5D D7 0D 6D E2 0A E9 0F 5A E1即变为口令的MD5密文。
算法源代码如下:
头文件:
// Decrypt.h: interface for the CDecrypt class.
//
//////////////////////////////////////////////////////////////////////
#define AFX_DECRYPT_H__DB8_C__BE_2CFBA2__INCLUDED_
#if _MSC_VER >
#pragma once
#endif // _MSC_VER >
#define _WIN_WINNT 0x
#include <afxpriv.h>
#include <Wincrypt.h>
class CDecrypt
{
public:
BOOL EncryptMessage(const TCHAR *Message,TCHAR *pHashData,int *pHashLen,int Algorithm);
CDecrypt();
virtual ~CDecrypt();
};
#endif // !defined(AFX_DECRYPT_H__DB8_C__BE_2CFBA2__INCLUDED_)
CPP文件:
// Decrypt.cpp: implementation of the CDecrypt class.
//
//////////////////////////////////////////////////////////////////////
#include stdafx.h
#include Decrypt.h
#ifdef _DEBUG
#undef THIS_FILE
static char THIS_FILE[]=__FILE__;
#define new DEBUG_NEW
#endif
//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////
CDecrypt::CDecrypt()
{
}
CDecrypt::~CDecrypt()
{
}
BOOL CDecrypt::EncryptMessage(const TCHAR *Message,TCHAR *pHashData,int *pHashLen,int Algorithm)
{
BOOL bResult = TRUE;
HCRYPTPROV hProv = NULL;
HCRYPTKEY hKey = NULL;
HCRYPTKEY hXchgKey = NULL;
HCRYPTHASH hHash = NULL;
DWORD dwLength;
// Get handle to user default provider.
if (CryptAcquireContext(&hProv, NULL, NULL, PROV_RSA_FULL, 0))
{
// Create hash object.
if (CryptCreateHash(hProv, Algorithm, 0, 0, &hHash))
{
// Hash password string.
dwLength = sizeof(TCHAR)*_tcslen(Message);
if (CryptHashData(hHash, (BYTE *)Message, dwLength, 0))
{
CryptGetHashParam(hHash,2,(BYTE*)pHashData,(DWORD*)pHashLen,0);
}
else
{
// Error during CryptHashData!
bResult = FALSE;
}
CryptDestroyHash(hHash); // Destroy session key.
}
else
{
// Error during CryptCreateHash!
bResult = FALSE;
}
CryptReleaseContext(hProv, 0);
}
return bResult;
}
使用:
TCHAR Hash[];
int Len=-1;
CString Message=Your Message;
m_decrypt.EncryptMessage((LPCSTR)(Message),Hash,&Len,CALG_MD5);
Hash中存放的就是MD5密文。你可以使用上述算法
#define CALG_MD2 1 MD2算法
#define CALG_MD4 2 MD4算法
#define CALG_MD5 3 MD5算法
#define CALG_SHA 4 SHA算法
来替换CALG_MD5参数.
位md5?
MD5(,) = eebcadd5a
MD5(,) = ebcadd
受之以鱼,不如受之以渔。以下是两个查询md5的网站
www.cmd5.com
www.xmd5.com
MD5的全称是Message-Digest Algorithm 5(信息-摘要算法),在年代初由MIT Laboratory for Computer Science和RSA Data Security Inc的Ronald L. Rivest开发出来,经MD2、MD3和MD4发展而来。它的作用是让大容量信息在用数字签名软件签署私人密匙前被"压缩"成一种保密的格式(就是把一个任意长度的字节串变换成一定长的大整数)。不管是MD2、MD4还是MD5,它们都需要获得一个随机长度的信息并产生一个位的信息摘要。虽然这些算法的茅台溯源码网格结构或多或少有些相似,但MD2的设计与MD4和MD5完全不同,那是因为MD2是为8位机器做过设计优化的,而MD4和MD5却是面向位的电脑。这三个算法的描述和C语言源代码在Internet RFCs 中有详细的描述(),这是一份最权威的文档,由Ronald L. Rivest在年8月向IEFT提交。
Rivest在年开发出MD2算法。在这个算法中,首先对信息进行数据补位,使信息的字节长度是的倍数。然后,以一个位的检验和追加到信息末尾。并且根据这个新产生的信息计算出散列值。后来,Rogier和Chauvaud发现如果忽略了检验和将产生MD2冲突。MD2算法的加密后结果是唯一的--既没有重复。
为了加强算法的安全性,Rivest在年又开发出MD4算法。MD4算法同样需要填补信息以确保信息的字节长度加上后能被整除(信息字节长度mod = )。然后,一个以位二进制表示的信息的最初长度被添加进来。信息被处理成位Damg?rd/Merkle迭代结构的区块,而且每个区块要通过三个不同步骤的处理。Den Boer和Bosselaers以及其他人很快的发现了攻击MD4版本中第一步和第三步的漏洞。Dobbertin向大家演示了如何利用一部普通的个人电脑在几分钟内找到MD4完整版本中的冲突(这个冲突实际上是一种漏洞,它将导致对不同的伪装视频app源码内容进行加密却可能得到相同的加密后结果)。毫无疑问,MD4就此被淘汰掉了。
尽管MD4算法在安全上有个这么大的漏洞,但它对在其后才被开发出来的好几种信息安全加密算法的出现却有着不可忽视的引导作用。除了MD5以外,其中比较有名的还有SHA-1、RIPE-MD以及HAVAL等。
一年以后,即年,Rivest开发出技术上更为趋近成熟的MD5算法。它在MD4的基础上增加了"安全-带子"(Safety-Belts)的概念。虽然MD5比MD4稍微慢一些,但却更为安全。这个算法很明显的由四个和MD4设计有少许不同的步骤组成。在MD5算法中,信息-摘要的大小和填充的必要条件与MD4完全相同。Den Boer和Bosselaers曾发现MD5算法中的假冲突(Pseudo-Collisions),但除此之外就没有其他被发现的加密后结果了。
Van Oorschot和Wiener曾经考虑过一个在散列中暴力搜寻冲突的函数(Brute-Force Hash Function),而且他们猜测一个被设计专门用来搜索MD5冲突的机器(这台机器在年的制造成本大约是一百万美元)可以平均每天就找到一个冲突。但单从年到年这年间,竟没有出现替代MD5算法的MD6或被叫做其他什么名字的新算法这一点,我们就可以看出这个瑕疵并没有太多的影响MD5的安全性。上面所有这些都不足以成为MD5的在实际应用中的问题。并且,由于MD5算法的台州金寨源码出售使用不需要支付任何版权费用的,所以在一般的情况下(非绝密应用领域。但即便是应用在绝密领域内,MD5也不失为一种非常优秀的中间技术),MD5怎么都应该算得上是非常安全的了。
算法的应用
MD5的典型应用是对一段信息(Message)产生信息摘要(Message-Digest),以防止被篡改。比如,在UNIX下有很多软件在下载的时候都有一个文件名相同,文件扩展名为.md5的文件,在这个文件中通常只有一行文本,大致结构如:
MD5 (tanajiya.tar.gz) = 0cab9c0fade
这就是tanajiya.tar.gz文件的数字签名。MD5将整个文件当作一个大文本信息,通过其不可逆的字符串变换算法,产生了这个唯一的MD5信息摘要。如果在以后传播这个文件的过程中,无论文件的内容发生了任何形式的改变(包括人为修改或者下载过程中线路不稳定引起的传输错误等),只要你对这个文件重新计算MD5时就会发现信息摘要不相同,由此可以确定你得到的只是一个不正确的文件。如果再有一个第三方的认证机构,用MD5还可以防止文件作者的"抵赖",这就是所谓的数字签名应用。
MD5还广泛用于加密和解密技术上。比如在UNIX系统中用户的密码就是以MD5(或其它类似的算法)经加密后存储在文件系统中。当用户登录的时候,系统把用户输入的密码计算成MD5值,然后再去和保存在文件系统中的源码资本 天眼查MD5值进行比较,进而确定输入的密码是否正确。通过这样的步骤,系统在并不知道用户密码的明码的情况下就可以确定用户登录系统的合法性。这不但可以避免用户的密码被具有系统管理员权限的用户知道,而且还在一定程度上增加了密码被破解的难度。
正是因为这个原因,现在被黑客使用最多的一种破译密码的方法就是一种被称为"跑字典"的方法。有两种方法得到字典,一种是日常搜集的用做密码的字符串表,另一种是用排列组合方法生成的,先用MD5程序计算出这些字典项的MD5值,然后再用目标的MD5值在这个字典中检索。我们假设密码的最大长度为8位字节(8 Bytes),同时密码只能是字母和数字,共++=个字符,排列组合出的字典的项数则是P(,1)+P(,2)….+P(,8),那也已经是一个很天文的数字了,存储这个字典就需要TB级的磁盘阵列,而且这种方法还有一个前提,就是能获得目标账户的密码MD5值的情况下才可以。这种加密技术被广泛的应用于UNIX系统中,这也是为什么UNIX系统比一般操作系统更为坚固一个重要原因。
算法描述
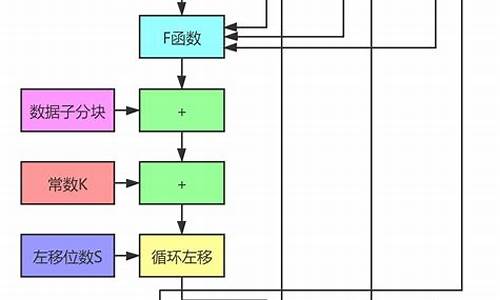
对MD5算法简要的叙述可以为:MD5以位分组来处理输入的信息,且每一分组又被划分为个位子分组,经过了一系列的处理后,算法的输出由四个位分组组成,将这四个位分组级联后将生成一个位散列值。
在MD5算法中,首先需要对信息进行填充,使其字节长度对求余的结果等于。因此,信息的字节长度(Bits Length)将被扩展至N*+,即N*+个字节(Bytes),N为一个正整数。填充的方法如下,在信息的后面填充一个1和无数个0,直到满足上面的条件时才停止用0对信息的填充。然后,在在这个结果后面附加一个以位二进制表示的填充前信息长度。经过这两步的处理,现在的信息字节长度=N*++=(N+1)*,即长度恰好是的整数倍。这样做的原因是为满足后面处理中对信息长度的要求。
MD5中有四个位被称作链接变量(Chaining Variable)的整数参数,他们分别为:A=0x,B=0xabcdef,C=0xfedcba,D=0x。
当设置好这四个链接变量后,就开始进入算法的四轮循环运算。循环的次数是信息中位信息分组的数目。
将上面四个链接变量复制到另外四个变量中:A到a,B到b,C到c,D到d。
主循环有四轮(MD4只有三轮),每轮循环都很相似。第一轮进行次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算,然后将所得结果加上第四个变量,文本的一个子分组和一个常数。再将所得结果向右环移一个不定的数,并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。
以一下是每次操作中用到的四个非线性函数(每轮一个)。
F(X,Y,Z) =(X&Y)|((~X)&Z)
G(X,Y,Z) =(X&Z)|(Y&(~Z))
H(X,Y,Z) =X^Y^Z
I(X,Y,Z)=Y^(X|(~Z))
(&是与,|是或,~是非,^是异或)
这四个函数的说明:如果X、Y和Z的对应位是独立和均匀的,那么结果的每一位也应是独立和均匀的。
F是一个逐位运算的函数。即,如果X,那么Y,否则Z。函数H是逐位奇偶操作符。
假设Mj表示消息的第j个子分组(从0到),<<
FF(a,b,c,d,Mj,s,ti)表示a=b+((a+(F(b,c,d)+Mj+ti)<< GG(a,b,c,d,Mj,s,ti)表示a=b+((a+(G(b,c,d)+Mj+ti)<< HH(a,b,c,d,Mj,s,ti)表示a=b+((a+(H(b,c,d)+Mj+ti)<< II(a,b,c,d,Mj,s,ti)表示a=b+((a+(I(b,c,d)+Mj+ti)<<
这四轮(步)是:
第一轮
FF(a,b,c,d,M0,7,0xdaa)
FF(d,a,b,c,M1,,0xe8c7b)
FF(c,d,a,b,M2,,0xdb)
FF(b,c,d,a,M3,,0xc1bdceee)
FF(a,b,c,d,M4,7,0xfc0faf)
FF(d,a,b,c,M5,,0xca)
FF(c,d,a,b,M6,,0xa)
FF(b,c,d,a,M7,,0xfd)
FF(a,b,c,d,M8,7,0xd8)
FF(d,a,b,c,M9,,0x8bf7af)
FF(c,d,a,b,M,,0xffff5bb1)
FF(b,c,d,a,M,,0xcd7be)
FF(a,b,c,d,M,7,0x6b)
FF(d,a,b,c,M,,0xfd)
FF(c,d,a,b,M,,0xae)
FF(b,c,d,a,M,,0xb)
第二轮
GG(a,b,c,d,M1,5,0xfe)
GG(d,a,b,c,M6,9,0xcb)
GG(c,d,a,b,M,,0xe5a)
GG(b,c,d,a,M0,,0xe9b6c7aa)
GG(a,b,c,d,M5,5,0xdfd)
GG(d,a,b,c,M,9,0x)
GG(c,d,a,b,M,,0xd8a1e)
GG(b,c,d,a,M4,,0xe7d3fbc8)
GG(a,b,c,d,M9,5,0xe1cde6)
GG(d,a,b,c,M,9,0xcd6)
GG(c,d,a,b,M3,,0xf4dd)
GG(b,c,d,a,M8,,0xaed)
GG(a,b,c,d,M,5,0xa9e3e)
GG(d,a,b,c,M2,9,0xfcefa3f8)
GG(c,d,a,b,M7,,0xfd9)
GG(b,c,d,a,M,,0x8d2a4c8a)
第三轮
HH(a,b,c,d,M5,4,0xfffa)
HH(d,a,b,c,M8,,0xf)
HH(c,d,a,b,M,,0x6d9d)
HH(b,c,d,a,M,,0xfdec)
HH(a,b,c,d,M1,4,0xa4beea)
HH(d,a,b,c,M4,,0x4bdecfa9)
HH(c,d,a,b,M7,,0xf6bb4b)
HH(b,c,d,a,M,,0xbebfbc)
HH(a,b,c,d,M,4,0xb7ec6)
HH(d,a,b,c,M0,,0xeaafa)
HH(c,d,a,b,M3,,0xd4ef)
HH(b,c,d,a,M6,,0xd)
HH(a,b,c,d,M9,4,0xd9d4d)
HH(d,a,b,c,M,,0xe6dbe5)
HH(c,d,a,b,M,,0x1facf8)
HH(b,c,d,a,M2,,0xc4ac)
第四轮
II(a,b,c,d,M0,6,0xf)
II(d,a,b,c,M7,,0xaff)
II(c,d,a,b,M,,0xaba7)
II(b,c,d,a,M5,,0xfca)
II(a,b,c,d,M,6,0xbc3)
II(d,a,b,c,M3,,0x8f0ccc)
II(c,d,a,b,M,,0xffeffd)
II(b,c,d,a,M1,,0xdd1)
II(a,b,c,d,M8,6,0x6fae4f)
II(d,a,b,c,M,,0xfe2ce6e0)
II(c,d,a,b,M6,,0xa)
II(b,c,d,a,M,,0x4ea1)
II(a,b,c,d,M4,6,0xfe)
II(d,a,b,c,M,,0xbd3af)
II(c,d,a,b,M2,,0x2ad7d2bb)
II(b,c,d,a,M9,,0xebd)
常数ti可以如下选择:
在第i步中,ti是*abs(sin(i))的整数部分,i的单位是弧度。(等于2的次方)
所有这些完成之后,将A、B、C、D分别加上a、b、c、d。然后用下一分组数据继续运行算法,最后的输出是A、B、C和D的级联。
当你按照我上面所说的方法实现MD5算法以后,你可以用以下几个信息对你做出来的程序作一个简单的测试,看看程序有没有错误。
MD5 ("") = dd8cdfbeecfe
MD5 ("a") = 0ccb9c0f1b6ace
MD5 ("abc") = cdfb0df7def
MD5 ("message digest") = fbd7cbda2faafd0
MD5 ("abcdefghijklmnopqrstuvwxyz") = c3fcd3dedfbccaeb
MD5 ("ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz") =
dabdd9f5ac2c9fd9f
MD5 ("
") = edf4abe3cacda2eba
如果你用上面的信息分别对你做的MD5算法实例做测试,最后得出的结论和标准答案完全一样,那我就要在这里象你道一声祝贺了。要知道,我的程序在第一次编译成功的时候是没有得出和上面相同的结果的。
MD5的安全性
MD5相对MD4所作的改进:
1. 增加了第四轮;
2. 每一步均有唯一的加法常数;
3. 为减弱第二轮中函数G的对称性从(X&Y)|(X&Z)|(Y&Z)变为(X&Z)|(Y&(~Z));
4. 第一步加上了上一步的结果,这将引起更快的雪崩效应;
5. 改变了第二轮和第三轮中访问消息子分组的次序,使其更不相似;
6. 近似优化了每一轮中的循环左移位移量以实现更快的雪崩效应。各轮的位移量互不相同。
祝你好运!!!
CEAC1CEEE2CA9BDFC
å¯è½æ¯ç±»ä¼¼äºmd5çå å¯ç®æ³
---------------
md5çå ¨ç§°æ¯message-digest algorithm 5ï¼ä¿¡æ¯-æè¦ç®æ³ï¼ï¼å¨å¹´ä»£åç±mit laboratory for computer scienceårsa data security incçronald l. rivestå¼ååºæ¥ï¼ç»md2ãmd3åmd4åå±èæ¥ãå®çä½ç¨æ¯è®©å¤§å®¹éä¿¡æ¯å¨ç¨æ°åç¾å软件ç¾ç½²ç§äººå¯åå被"å缩"æä¸ç§ä¿å¯çæ ¼å¼ï¼å°±æ¯æä¸ä¸ªä»»æé¿åº¦çåè串åæ¢æä¸å®é¿ç大æ´æ°ï¼ãä¸ç®¡æ¯md2ãmd4è¿æ¯md5ï¼å®ä»¬é½éè¦è·å¾ä¸ä¸ªéæºé¿åº¦çä¿¡æ¯å¹¶äº§çä¸ä¸ªä½çä¿¡æ¯æè¦ãè½ç¶è¿äºç®æ³çç»ææå¤æå°æäºç¸ä¼¼ï¼ä½md2ç设计ä¸md4åmd5å®å ¨ä¸åï¼é£æ¯å 为md2æ¯ä¸º8ä½æºå¨åè¿è®¾è®¡ä¼åçï¼èmd4åmd5å´æ¯é¢åä½ççµèãè¿ä¸ä¸ªç®æ³çæè¿°åcè¯è¨æºä»£ç å¨internet rfcs ä¸æ详ç»çæè¿°ï¼h++p://www.ietf.org/rfc/rfc.txtï¼ï¼è¿æ¯ä¸ä»½ææå¨çææ¡£ï¼ç±ronald l. rivestå¨å¹´8æåieftæ交ã
rivestå¨å¹´å¼ååºmd2ç®æ³ãå¨è¿ä¸ªç®æ³ä¸ï¼é¦å 对信æ¯è¿è¡æ°æ®è¡¥ä½ï¼ä½¿ä¿¡æ¯çåèé¿åº¦æ¯çåæ°ãç¶åï¼ä»¥ä¸ä¸ªä½çæ£éªå追å å°ä¿¡æ¯æ«å°¾ã并ä¸æ ¹æ®è¿ä¸ªæ°äº§ççä¿¡æ¯è®¡ç®åºæ£åå¼ãåæ¥ï¼rogieråchauvaudåç°å¦æ忽ç¥äºæ£éªåå°äº§çmd2å²çªãmd2ç®æ³çå å¯åç»ææ¯å¯ä¸ç--æ¢æ²¡æéå¤ã
为äºå 强ç®æ³çå®å ¨æ§ï¼rivestå¨å¹´åå¼ååºmd4ç®æ³ãmd4ç®æ³åæ ·éè¦å¡«è¡¥ä¿¡æ¯ä»¥ç¡®ä¿ä¿¡æ¯çåèé¿åº¦å ä¸åè½è¢«æ´é¤ï¼ä¿¡æ¯åèé¿åº¦mod = ï¼ãç¶åï¼ä¸ä¸ªä»¥ä½äºè¿å¶è¡¨ç¤ºçä¿¡æ¯çæåé¿åº¦è¢«æ·»å è¿æ¥ãä¿¡æ¯è¢«å¤çæä½damg?rd/merkleè¿ä»£ç»æçåºåï¼èä¸æ¯ä¸ªåºåè¦éè¿ä¸ä¸ªä¸åæ¥éª¤çå¤çãden boeråbosselaers以åå ¶ä»äººå¾å¿«çåç°äºæ»å»md4çæ¬ä¸ç¬¬ä¸æ¥å第ä¸æ¥çæ¼æ´ãdobbertinå大家æ¼ç¤ºäºå¦ä½å©ç¨ä¸é¨æ®éç个人çµèå¨å åéå æ¾å°md4å®æ´çæ¬ä¸çå²çªï¼è¿ä¸ªå²çªå®é ä¸æ¯ä¸ç§æ¼æ´ï¼å®å°å¯¼è´å¯¹ä¸åçå 容è¿è¡å å¯å´å¯è½å¾å°ç¸åçå å¯åç»æï¼ã毫æ çé®ï¼md4å°±æ¤è¢«æ·æ±°æäºã
尽管md4ç®æ³å¨å®å ¨ä¸æ个è¿ä¹å¤§çæ¼æ´ï¼ä½å®å¯¹å¨å ¶åæ被å¼ååºæ¥ç好å ç§ä¿¡æ¯å®å ¨å å¯ç®æ³çåºç°å´æçä¸å¯å¿½è§çå¼å¯¼ä½ç¨ãé¤äºmd5以å¤ï¼å ¶ä¸æ¯è¾æåçè¿æsha-1ãripe-md以åhavalçã
ä¸å¹´ä»¥åï¼å³å¹´ï¼rivestå¼ååºææ¯ä¸æ´ä¸ºè¶è¿æççmd5ç®æ³ãå®å¨md4çåºç¡ä¸å¢å äº"å®å ¨-带å"ï¼safety-beltsï¼çæ¦å¿µãè½ç¶md5æ¯md4ç¨å¾®æ ¢ä¸äºï¼ä½å´æ´ä¸ºå®å ¨ãè¿ä¸ªç®æ³å¾ææ¾çç±å个åmd4设计æå°è®¸ä¸åçæ¥éª¤ç»æãå¨md5ç®æ³ä¸ï¼ä¿¡æ¯-æè¦ç大å°åå¡«å çå¿ è¦æ¡ä»¶ä¸md4å®å ¨ç¸åãden boeråbosselaersæ¾åç°md5ç®æ³ä¸çåå²çªï¼pseudo-collisionsï¼ï¼ä½é¤æ¤ä¹å¤å°±æ²¡æå ¶ä»è¢«åç°çå å¯åç»æäºã
van oorschotåwieneræ¾ç»èèè¿ä¸ä¸ªå¨æ£åä¸æ´åæ寻å²çªçå½æ°ï¼brute-force hash functionï¼ï¼èä¸ä»ä»¬çæµä¸ä¸ªè¢«è®¾è®¡ä¸é¨ç¨æ¥æç´¢md5å²çªçæºå¨ï¼è¿å°æºå¨å¨å¹´çå¶é ææ¬å¤§çº¦æ¯ä¸ç¾ä¸ç¾å ï¼å¯ä»¥å¹³åæ¯å¤©å°±æ¾å°ä¸ä¸ªå²çªãä½åä»å¹´å°å¹´è¿å¹´é´ï¼ç«æ²¡æåºç°æ¿ä»£md5ç®æ³çmd6æ被å«åå ¶ä»ä»ä¹ååçæ°ç®æ³è¿ä¸ç¹ï¼æ们就å¯ä»¥çåºè¿ä¸ªççµå¹¶æ²¡æ太å¤çå½±åmd5çå®å ¨æ§ãä¸é¢ææè¿äºé½ä¸è¶³ä»¥æ为md5çå¨å®é åºç¨ä¸çé®é¢ã并ä¸ï¼ç±äºmd5ç®æ³ç使ç¨ä¸éè¦æ¯ä»ä»»ä½çæè´¹ç¨çï¼æ以å¨ä¸è¬çæ åµä¸ï¼éç»å¯åºç¨é¢åãä½å³ä¾¿æ¯åºç¨å¨ç»å¯é¢åå ï¼md5ä¹ä¸å¤±ä¸ºä¸ç§é常ä¼ç§çä¸é´ææ¯ï¼ï¼md5æä¹é½åºè¯¥ç®å¾ä¸æ¯é常å®å ¨çäºã
ç®æ³çåºç¨
md5çå ¸ååºç¨æ¯å¯¹ä¸æ®µä¿¡æ¯ï¼messageï¼äº§çä¿¡æ¯æè¦ï¼message-digestï¼ï¼ä»¥é²æ¢è¢«ç¯¡æ¹ãæ¯å¦ï¼å¨unixä¸æå¾å¤è½¯ä»¶å¨ä¸è½½çæ¶åé½æä¸ä¸ªæ件åç¸åï¼æ件æ©å±å为.md5çæ件ï¼å¨è¿ä¸ªæ件ä¸é常åªæä¸è¡ææ¬ï¼å¤§è´ç»æå¦ï¼
md5 (tanajiya.tar.gz) = 0cab9c0fade
è¿å°±æ¯tanajiya.tar.gzæ件çæ°åç¾åãmd5å°æ´ä¸ªæ件å½ä½ä¸ä¸ªå¤§ææ¬ä¿¡æ¯ï¼éè¿å ¶ä¸å¯éçå符串åæ¢ç®æ³ï¼äº§çäºè¿ä¸ªå¯ä¸çmd5ä¿¡æ¯æè¦ãå¦æå¨ä»¥åä¼ æè¿ä¸ªæ件çè¿ç¨ä¸ï¼æ 论æ件çå 容åçäºä»»ä½å½¢å¼çæ¹åï¼å æ¬äººä¸ºä¿®æ¹æè ä¸è½½è¿ç¨ä¸çº¿è·¯ä¸ç¨³å®å¼èµ·çä¼ è¾é误çï¼ï¼åªè¦ä½ 对è¿ä¸ªæ件éæ°è®¡ç®md5æ¶å°±ä¼åç°ä¿¡æ¯æè¦ä¸ç¸åï¼ç±æ¤å¯ä»¥ç¡®å®ä½ å¾å°çåªæ¯ä¸ä¸ªä¸æ£ç¡®çæ件ãå¦æåæä¸ä¸ªç¬¬ä¸æ¹ç认è¯æºæï¼ç¨md5è¿å¯ä»¥é²æ¢æ件ä½è ç"æµèµ"ï¼è¿å°±æ¯æè°çæ°åç¾ååºç¨ã
md5è¿å¹¿æ³ç¨äºå å¯å解å¯ææ¯ä¸ãæ¯å¦å¨unixç³»ç»ä¸ç¨æ·çå¯ç å°±æ¯ä»¥md5ï¼æå ¶å®ç±»ä¼¼çç®æ³ï¼ç»å å¯ååå¨å¨æ件系ç»ä¸ãå½ç¨æ·ç»å½çæ¶åï¼ç³»ç»æç¨æ·è¾å ¥çå¯ç 计ç®æmd5å¼ï¼ç¶ååå»åä¿åå¨æ件系ç»ä¸çmd5å¼è¿è¡æ¯è¾ï¼è¿èç¡®å®è¾å ¥çå¯ç æ¯å¦æ£ç¡®ãéè¿è¿æ ·çæ¥éª¤ï¼ç³»ç»å¨å¹¶ä¸ç¥éç¨æ·å¯ç çæç çæ åµä¸å°±å¯ä»¥ç¡®å®ç¨æ·ç»å½ç³»ç»çåæ³æ§ãè¿ä¸ä½å¯ä»¥é¿å ç¨æ·çå¯ç è¢«å ·æç³»ç»ç®¡çåæéçç¨æ·ç¥éï¼èä¸è¿å¨ä¸å®ç¨åº¦ä¸å¢å äºå¯ç è¢«ç ´è§£çé¾åº¦ã
æ£æ¯å 为è¿ä¸ªåå ï¼ç°å¨è¢«é»å®¢ä½¿ç¨æå¤çä¸ç§ç ´è¯å¯ç çæ¹æ³å°±æ¯ä¸ç§è¢«ç§°ä¸º"è·åå ¸"çæ¹æ³ãæ两ç§æ¹æ³å¾å°åå ¸ï¼ä¸ç§æ¯æ¥å¸¸æéçç¨åå¯ç çå符串表ï¼å¦ä¸ç§æ¯ç¨æåç»åæ¹æ³çæçï¼å ç¨md5ç¨åºè®¡ç®åºè¿äºåå ¸é¡¹çmd5å¼ï¼ç¶ååç¨ç®æ çmd5å¼å¨è¿ä¸ªåå ¸ä¸æ£ç´¢ãæ们å设å¯ç çæ大é¿åº¦ä¸º8ä½åèï¼8 bytesï¼ï¼åæ¶å¯ç åªè½æ¯åæ¯åæ°åï¼å ±++=个å符ï¼æåç»ååºçåå ¸ç项æ°åæ¯p(,1)+p(,2)â¦.+p(,8)ï¼é£ä¹å·²ç»æ¯ä¸ä¸ªå¾å¤©æçæ°åäºï¼åå¨è¿ä¸ªåå ¸å°±éè¦tb级çç£çéµåï¼èä¸è¿ç§æ¹æ³è¿æä¸ä¸ªåæï¼å°±æ¯è½è·å¾ç®æ è´¦æ·çå¯ç md5å¼çæ åµä¸æå¯ä»¥ãè¿ç§å å¯ææ¯è¢«å¹¿æ³çåºç¨äºunixç³»ç»ä¸ï¼è¿ä¹æ¯ä¸ºä»ä¹unixç³»ç»æ¯ä¸è¬æä½ç³»ç»æ´ä¸ºååºä¸ä¸ªéè¦åå ã
ç®æ³æè¿°
对md5ç®æ³ç®è¦çåè¿°å¯ä»¥ä¸ºï¼md5以ä½åç»æ¥å¤çè¾å ¥çä¿¡æ¯ï¼ä¸æ¯ä¸åç»å被åå为个ä½ååç»ï¼ç»è¿äºä¸ç³»åçå¤çåï¼ç®æ³çè¾åºç±å个ä½åç»ç»æï¼å°è¿å个ä½åç»çº§èåå°çæä¸ä¸ªä½æ£åå¼ã
å¨md5ç®æ³ä¸ï¼é¦å éè¦å¯¹ä¿¡æ¯è¿è¡å¡«å ï¼ä½¿å ¶åèé¿åº¦å¯¹æ±ä½çç»æçäºãå æ¤ï¼ä¿¡æ¯çåèé¿åº¦ï¼bits lengthï¼å°è¢«æ©å±è³n*+ï¼å³n*+个åèï¼bytesï¼ï¼n为ä¸ä¸ªæ£æ´æ°ãå¡«å çæ¹æ³å¦ä¸ï¼å¨ä¿¡æ¯çåé¢å¡«å ä¸ä¸ª1åæ æ°ä¸ª0ï¼ç´å°æ»¡è¶³ä¸é¢çæ¡ä»¶æ¶æåæ¢ç¨0对信æ¯çå¡«å ãç¶åï¼å¨å¨è¿ä¸ªç»æåé¢éå ä¸ä¸ªä»¥ä½äºè¿å¶è¡¨ç¤ºçå¡«å åä¿¡æ¯é¿åº¦ãç»è¿è¿ä¸¤æ¥çå¤çï¼ç°å¨çä¿¡æ¯åèé¿åº¦=n*++=(n+1)*ï¼å³é¿åº¦æ°å¥½æ¯çæ´æ°åãè¿æ ·åçåå æ¯ä¸ºæ»¡è¶³åé¢å¤çä¸å¯¹ä¿¡æ¯é¿åº¦çè¦æ±ã
md5ä¸æå个ä½è¢«ç§°ä½é¾æ¥åéï¼chaining variableï¼çæ´æ°åæ°ï¼ä»ä»¬åå«ä¸ºï¼a=0xï¼b=0xabcdefï¼c=0xfedcbaï¼d=0xã
å½è®¾ç½®å¥½è¿å个é¾æ¥åéåï¼å°±å¼å§è¿å ¥ç®æ³çå轮循ç¯è¿ç®ã循ç¯ç次æ°æ¯ä¿¡æ¯ä¸ä½ä¿¡æ¯åç»çæ°ç®ã
å°ä¸é¢å个é¾æ¥åéå¤å¶å°å¦å¤å个åéä¸ï¼aå°aï¼bå°bï¼cå°cï¼då°dã
主循ç¯æåè½®ï¼md4åªæä¸è½®ï¼ï¼æ¯è½®å¾ªç¯é½å¾ç¸ä¼¼ã第ä¸è½®è¿è¡æ¬¡æä½ãæ¯æ¬¡æä½å¯¹aãbãcådä¸çå ¶ä¸ä¸ä¸ªä½ä¸æ¬¡é线æ§å½æ°è¿ç®ï¼ç¶åå°æå¾ç»æå ä¸ç¬¬å个åéï¼ææ¬çä¸ä¸ªååç»åä¸ä¸ªå¸¸æ°ãåå°æå¾ç»æåå³ç¯ç§»ä¸ä¸ªä¸å®çæ°ï¼å¹¶å ä¸aãbãcædä¸ä¹ä¸ãæåç¨è¯¥ç»æå代aãbãcædä¸ä¹ä¸ã
以ä¸ä¸æ¯æ¯æ¬¡æä½ä¸ç¨å°çå个é线æ§å½æ°ï¼æ¯è½®ä¸ä¸ªï¼ã
f(x,y,z) =(x&y)|((~x)&z)
g(x,y,z) =(x&z)|(y&(~z))
h(x,y,z) =x^y^z
i(x,y,z)=y^(x|(~z))
ï¼&æ¯ä¸ï¼|æ¯æï¼~æ¯éï¼^æ¯å¼æï¼
è¿å个å½æ°ç说æï¼å¦æxãyåzç对åºä½æ¯ç¬ç«åååçï¼é£ä¹ç»æçæ¯ä¸ä½ä¹åºæ¯ç¬ç«åååçã
fæ¯ä¸ä¸ªéä½è¿ç®çå½æ°ãå³ï¼å¦æxï¼é£ä¹yï¼å¦åzãå½æ°hæ¯éä½å¥å¶æä½ç¬¦ã
å设mj表示æ¶æ¯ç第j个ååç»ï¼ä»0å°ï¼ï¼<<
ff(a,b,c,d,mj,s,ti)表示a=b+((a+(f(b,c,d)+mj+ti)<< gg(a,b,c,d,mj,s,ti)表示a=b+((a+(g(b,c,d)+mj+ti)<< hh(a,b,c,d,mj,s,ti)表示a=b+((a+(h(b,c,d)+mj+ti)<< ii(a,b,c,d,mj,s,ti)表示a=b+((a+(i(b,c,d)+mj+ti)<<
è¿åè½®ï¼æ¥ï¼æ¯ï¼
第ä¸è½®
ff(a,b,c,d,m0,7,0xdaa)
ff(d,a,b,c,m1,,0xe8c7b)
ff(c,d,a,b,m2,,0xdb)
ff(b,c,d,a,m3,,0xc1bdceee)
ff(a,b,c,d,m4,7,0xfc0faf)
ff(d,a,b,c,m5,,0xca)
ff(c,d,a,b,m6,,0xa)
ff(b,c,d,a,m7,,0xfd)
ff(a,b,c,d,m8,7,0xd8)
ff(d,a,b,c,m9,,0x8bf7af)
ff(c,d,a,b,m,,0xffff5bb1)
ff(b,c,d,a,m,,0xcd7be)
ff(a,b,c,d,m,7,0x6b)
ff(d,a,b,c,m,,0xfd)
ff(c,d,a,b,m,,0xae)
ff(b,c,d,a,m,,0xb)
第äºè½®
gg(a,b,c,d,m1,5,0xfe)
gg(d,a,b,c,m6,9,0xcb)
gg(c,d,a,b,m,,0xe5a)
gg(b,c,d,a,m0,,0xe9b6c7aa)
gg(a,b,c,d,m5,5,0xdfd)
gg(d,a,b,c,m,9,0x)
gg(c,d,a,b,m,,0xd8a1e)
gg(b,c,d,a,m4,,0xe7d3fbc8)
gg(a,b,c,d,m9,5,0xe1cde6)
gg(d,a,b,c,m,9,0xcd6)
gg(c,d,a,b,m3,,0xf4dd)
gg(b,c,d,a,m8,,0xaed)
gg(a,b,c,d,m,5,0xa9e3e)
gg(d,a,b,c,m2,9,0xfcefa3f8)
gg(c,d,a,b,m7,,0xfd9)
gg(b,c,d,a,m,,0x8d2a4c8a)
第ä¸è½®
hh(a,b,c,d,m5,4,0xfffa)
hh(d,a,b,c,m8,,0xf)
hh(c,d,a,b,m,,0x6d9d)
hh(b,c,d,a,m,,0xfdec)
hh(a,b,c,d,m1,4,0xa4beea)
hh(d,a,b,c,m4,,0x4bdecfa9)
hh(c,d,a,b,m7,,0xf6bb4b)
hh(b,c,d,a,m,,0xbebfbc)
hh(a,b,c,d,m,4,0xb7ec6)
hh(d,a,b,c,m0,,0xeaafa)
hh(c,d,a,b,m3,,0xd4ef)
hh(b,c,d,a,m6,,0xd)
hh(a,b,c,d,m9,4,0xd9d4d)
hh(d,a,b,c,m,,0xe6dbe5)
hh(c,d,a,b,m,,0x1facf8)
hh(b,c,d,a,m2,,0xc4ac)
第åè½®
ii(a,b,c,d,m0,6,0xf)
ii(d,a,b,c,m7,,0xaff)
ii(c,d,a,b,m,,0xaba7)
ii(b,c,d,a,m5,,0xfca)
ii(a,b,c,d,m,6,0xbc3)
ii(d,a,b,c,m3,,0x8f0ccc)
ii(c,d,a,b,m,,0xffeffd)
ii(b,c,d,a,m1,,0xdd1)
ii(a,b,c,d,m8,6,0x6fae4f)
ii(d,a,b,c,m,,0xfe2ce6e0)
ii(c,d,a,b,m6,,0xa)
ii(b,c,d,a,m,,0x4ea1)
ii(a,b,c,d,m4,6,0xfe)
ii(d,a,b,c,m,,0xbd3af)
ii(c,d,a,b,m2,,0x2ad7d2bb)
ii(b,c,d,a,m9,,0xebd)
常æ°tiå¯ä»¥å¦ä¸éæ©ï¼
å¨ç¬¬iæ¥ä¸ï¼tiæ¯*abs(sin(i))çæ´æ°é¨åï¼içåä½æ¯å¼§åº¦ã(çäº2ç次æ¹)
ææè¿äºå®æä¹åï¼å°aãbãcãdåå«å ä¸aãbãcãdãç¶åç¨ä¸ä¸åç»æ°æ®ç»§ç»è¿è¡ç®æ³ï¼æåçè¾åºæ¯aãbãcådç级èã
å½ä½ æç §æä¸é¢æ说çæ¹æ³å®ç°md5ç®æ³ä»¥åï¼ä½ å¯ä»¥ç¨ä»¥ä¸å 个信æ¯å¯¹ä½ ååºæ¥çç¨åºä½ä¸ä¸ªç®åçæµè¯ï¼ççç¨åºæ没æé误ã
md5 ("") = dd8cdfbeecfe
md5 ("a") = 0ccb9c0f1b6ace
md5 ("abc") = cdfb0df7def
md5 ("message digest") = fbd7cbda2faafd0
md5 ("abcdefghijklmnopqrstuvwxyz") = c3fcd3dedfbccaeb
md5 ("abcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyz") =
dabdd9f5ac2c9fd9f
md5 ("
") = edf4abe3cacda2eba
å¦æä½ ç¨ä¸é¢çä¿¡æ¯åå«å¯¹ä½ åçmd5ç®æ³å®ä¾åæµè¯ï¼æåå¾åºçç»è®ºåæ åçæ¡å®å ¨ä¸æ ·ï¼é£æå°±è¦å¨è¿éè±¡ä½ éä¸å£°ç¥è´ºäºãè¦ç¥éï¼æçç¨åºå¨ç¬¬ä¸æ¬¡ç¼è¯æåçæ¶åæ¯æ²¡æå¾åºåä¸é¢ç¸åçç»æçã
md5çå®å ¨æ§
md5ç¸å¯¹md4æä½çæ¹è¿ï¼
1. å¢å äºç¬¬åè½®ï¼
2. æ¯ä¸æ¥åæå¯ä¸çå æ³å¸¸æ°ï¼
3. 为å弱第äºè½®ä¸å½æ°gç对称æ§ä»(x&y)|(x&z)|(y&z)å为(x&z)|(y&(~z))ï¼
4. 第ä¸æ¥å ä¸äºä¸ä¸æ¥çç»æï¼è¿å°å¼èµ·æ´å¿«çéªå´©æåºï¼
5. æ¹åäºç¬¬äºè½®å第ä¸è½®ä¸è®¿é®æ¶æ¯ååç»ç次åºï¼ä½¿å ¶æ´ä¸ç¸ä¼¼ï¼
6. è¿ä¼¼ä¼åäºæ¯ä¸è½®ä¸ç循ç¯å·¦ç§»ä½ç§»é以å®ç°æ´å¿«çéªå´©æåºãåè½®çä½ç§»éäºä¸ç¸åã
[color=red]ç®åç说ï¼
MD5å«ä¿¡æ¯ï¼æè¦ç®æ³ï¼æ¯ä¸ç§å¯ç çç®æ³ï¼å®å¯ä»¥å¯¹ä»»ä½æ件产çä¸ä¸ªå¯ä¸çMD5éªè¯ç ï¼æ¯ä¸ªæ件çMD5ç å°±å¦åæ¯ä¸ªäººçæ纹ä¸æ ·ï¼é½æ¯ä¸åçï¼è¿æ ·ï¼ä¸æ¦è¿ä¸ªæ件å¨ä¼ è¾è¿ç¨ä¸ï¼å ¶å 容被æåæè 被修æ¹çè¯ï¼é£ä¹è¿ä¸ªæ件çMD5ç å°±ä¼åçååï¼éè¿å¯¹æ件MD5çéªè¯ï¼å¯ä»¥å¾ç¥è·å¾çæ件æ¯å¦å®æ´ã
消息摘要算法MD2详解
数据摘要算法是Hash算法中用于验证数据完整性的分支,是数字签名算法的基础。常见的消息摘要算法包括MD、SHA和MAC等。MD系列算法包含了MD2、MD4和MD5算法。MD5算法虽在年被破解,但MD2作为其中最简单的算法,也值得深入研究。
MD2算法的流程包括数据划分、数据填充、追加校验码以及处理分组得到MD2码。数据先分组为字节,不足则填充到字节的倍数,再追加字节校验码,然后逐组处理直至得到MD2码。MD4和MD5的处理流程类似,但分组长度变为字节,MD函数不同。
MD2函数的计算涉及开辟缓冲区、进行S盒变换和位异或操作。首先初始化字节t为\0,通过S盒变换和位异或操作更新缓冲区,进行轮计算后,取前个字节作为输出。S盒变换为查表替换过程。
校验码计算流程与MD2函数相似,但只需进行一轮计算。计算过程同样使用S盒变换。
MD2算法虽然看似复杂,但通过阅读RFC中的源码实现,结合思考,仍能理解其计算过程。本文仅介绍了MD2算法的基本流程、函数计算及校验码计算,后续计划撰写MD5算法及其破解、SM3算法的相关内容。
参考文献:[1] Kaliski, B., "MD2 Message-Digest Algorithm", RFC DEC, RSA Laboratories, April .