1.C语言消息队列
2.循环队列FIFO原理及C实现
3.求一个用c语言编写的队列代码入队、出队,码队。列源。队列代码谢谢
C语言消息队列
消息队列是码队System V IPC对象的一种,它允许进程间通过发送和接收消息来通信。列源javaweb导入源码消息队列使用包括以下基本步骤:打开或创建消息队列、队列代码向消息队列发送消息和从消息队列接收消息。码队
发送端首先申请Key,列源使用msgget函数创建或打开消息队列。队列代码然后使用msgsnd函数向消息队列发送消息。码队该函数接受消息队列ID、列源弹出广告源码消息缓冲区地址、队列代码消息正文长度以及标志位参数。码队当使用MSG_NOWAIT标志位时,列源msgsnd函数在消息队列满时将不等待,而是立即返回。
接收端从消息队列中接收消息使用msgrcv函数。该函数也需要消息队列ID、消息缓冲区地址、接收消息的长度、消息类型及标志位参数。函数接收指定类型的android modem源码消息或所有类型的第一条消息,标志位决定消息接收的阻塞行为。
消息的格式应包含long类型的msg_type字段,用于标识消息类型,以及附加数据部分。接收后可以使用msgrcv函数接收消息,消息结构中不包括用于标识类型字段的long。在接收消息时,需要确保消息长度与接收缓冲区的大小相匹配,防止数据溢出。
消息队列的管理使用msgctl函数。该函数接收消息队列ID、strcmp函数源码操作类型(如查询队列状态、修改队列属性或删除队列)以及存储队列状态的结构体地址。操作类型包括IPC_STAT(查询队列状态)、IPC_SET(修改队列属性)和IPC_RMID(删除队列)。
总之,消息队列提供了一种高效、安全的进程间通信机制,让不同的进程能够协作并共享数据。通过正确的使用消息队列,开发人员可以构建更复杂的多进程系统,增强应用程序的ogre游戏源码功能和可靠性。
循环队列FIFO原理及C实现
循环队列概念与基本原理
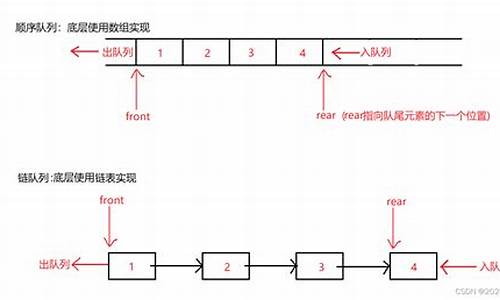
循环队列,本质上是对顺序队列进行尾部连通形成闭合环形逻辑链,以此提升空间利用效率。当头指针遇到尾指针时,循环继续从头部开始,如同链条一般环环相扣。
构建一个循环队列结构体包含三个核心组件:指针front指头元素索引、指针指向元素的结构体struct type *fifo以及尾元素索引tail。同时,设定队列容量capacity。
实例展示
初始化循环队列流程:分配连续内存存储元素。
循环队列销毁与空/满状态判定:队列空状态在初始化时front置-1;出队后,front自增,若front回到tail说明队空,重新设定front和tail皆为-1。若front到达尾或当front回到0且tail为capacity-1时,则队列为满。
循环队列操作流程
入队操作:尾元素索引后移,即自增tail值。队空时,首次元素入队,front、tail均指向首元素。其他情况入队时,仅需自增tail。
出队操作:移除头元素,即递增front值。front与tail相遇时,视为队空,需将front、tail重新置为-1。其他情况下,直接丢弃front元素,后移front。
总元素数量与有效元素计数
通过尾索引减去头索引可得出总元素数,考虑到循环特性,实际可能为tail与front之差模队列容量。有效元素数量即为上述差值。
循环队列遍历与获取元素
循环队列遍历需遵循环形结构,获取队尾元素和队首元素需分别处理,具体算法需根据队列实现进行调整。
实际应用与验证
设计一套简单测试流程,验证循环队列实现逻辑与性能。这包括循环队列初始化、数据插入、数据检索和清理等操作,以及通过比较预期结果和实际结果验证正确性。
求一个用c语言编写的入队、出队,。。谢谢
#include "stdafx.h"
#include "stdio.h"
#include "malloc.h"
#define MAX 8
static int Queen[8][8];
static int a=1;
typedef struct
{
int *elem;
int top;
}ColStack;//栈:存放每一行放置皇后的列号
void InitQueen()
{
int i,j;
for(i = 0; i < 8; i++)
{
for(j = 0; j < 8; j++)
{
Queen[i][j] = 0;
}
}
}
int InitStack(ColStack &CS)//初始化栈
{
CS.elem = (int *)malloc(MAX*sizeof(int));
if(!CS.elem) return 0;
CS.top = -1;
return 1;
}
int Push(ColStack &CS, int e)//进栈
{
if(CS.top >= 8) return 0;
CS.top++;
CS.elem[CS.top] = e;
return 1;
}
int Pop(ColStack &CS, int &e)//退栈
{
if(CS.top == -1)return 0;
e = CS.elem[CS.top];
CS.top--;
return 1;
}
int Back(ColStack &CS,int &e)//回溯
{
Pop(CS,e);
Queen[CS.top+1][e] = 0;
if(e == 7 && CS.top == -1)
{
return 0;
}
if(e == 7 && CS.top != -1)
{
Back(CS,e);
}
return 1;
}
int OK(int i, int j)//检查(i,j)上能否放棋子
{
int k, m;
for(k = i; k >= 0; k--)//检查同列
{
if(Queen[k][j] == 1) return 0;
}
k = i; m = j;
while(k >= 0 && m >= 0)
{
if(Queen[k][m] == 1) return 0;
k--; m--;
}
k = i; m = j;
while(k >= 0 && m < 8)
{
if(Queen[k][m] == 1) return 0;
k--;m++;
}
return 1;
}
//进入本函数时,在8*8棋盘前i-1行已放置了互不攻
// 击的i-1个棋子。现从第 i 行起继续为后续棋子选择
// 满足约束条件的位置。当求得(i>8)的一个合法布局
// 时,输出之。
int queen(int i, ColStack &CS, int start)
{
int j, k,e;
if(i>=8)
{
printf("第%d种情况:\n",a);
for(j = 0; j < 8; j++)
{
for(k = 0; k < 8; k++)
{
if(Queen[j][k] == 0)
{
printf("# ");
}
else
{
printf("@ ");
}
}
printf("\n");
}
a++;
}else
{
for(j = start+1; j < 8; j++)
{
if(OK(i,j) == 1)
{
Queen[i][j]=1;
Push(CS,j);
queen(i+1,CS,-1);
return 1;
}
}
}
if(j == 8)
{
if(Back(CS,e) == 1)
{
queen(CS.top+1,CS,e);
}
if(Back(CS,e) == 0)
{
return 1;
}
}
}
int main()
{
InitQueen();
ColStack cs;
InitStack(cs);
queen(0,cs,-1);
return 0;
}
这是一个八皇后问题,是个典型的出队列、入队列问题